Provable limitations of deep learning
Paper and Code
Dec 16, 2018
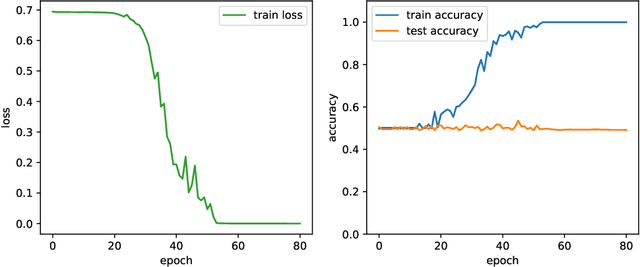
As the success of deep learning reaches more grounds, one would like to also envision the potential limits of deep learning. This paper gives a first set of results proving that deep learning algorithms fail at learning certain efficiently learnable functions. Parity functions form the running example of our results and the paper puts forward a notion of low cross-predictability that defines a more general class of functions for which such failures tend to generalize (with examples in community detection and arithmetic learning). Recall that it is known that the class of neural networks (NNs) with polynomial network size can express any function that can be implemented in polynomial time, and that their sample complexity scales polynomially with the network size. The challenge is with the optimization error (the ERM is NP-hard), and the success behind deep learning is to train deep NNs with descent algorithms. The failures shown in this paper apply to training poly-size NNs on function distributions of low cross-predictability with a descent algorithm that is either run with limited memory per sample or that is initialized and run with enough randomness (exponentially small for GD). We further claim that such types of constraints are necessary to obtain failures, in that exact SGD with careful non-random initialization can learn parities. The cross-predictability notion has some similarity with the statistical dimension used in statistical query (SQ) algorithms, however the two definitions are different for reasons explained in the paper. The proof techniques are based on exhibiting algorithmic constraints that imply a statistical indistinguishability between the algorithm's output on the test model v.s.\ a null model, using information measures to bound the total variation distance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge