Provable Imbalanced Point Clustering
Paper and Code
Aug 26, 2024
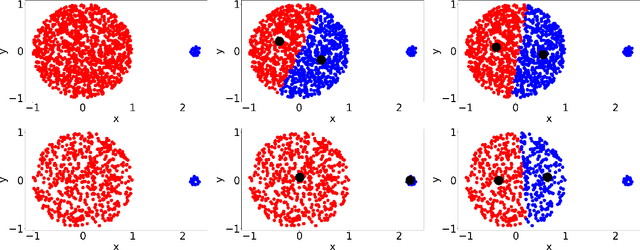

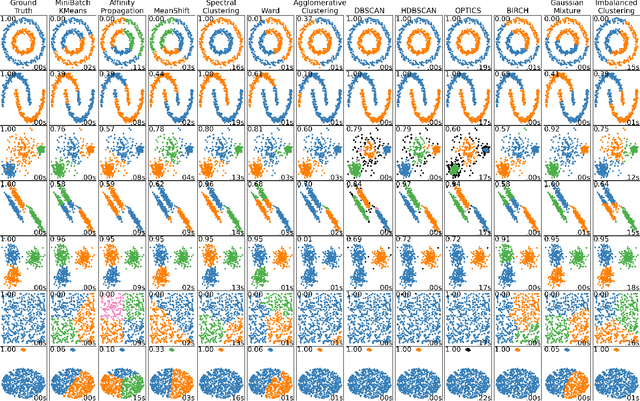
We suggest efficient and provable methods to compute an approximation for imbalanced point clustering, that is, fitting $k$-centers to a set of points in $\mathbb{R}^d$, for any $d,k\geq 1$. To this end, we utilize \emph{coresets}, which, in the context of the paper, are essentially weighted sets of points in $\mathbb{R}^d$ that approximate the fitting loss for every model in a given set, up to a multiplicative factor of $1\pm\varepsilon$. We provide [Section 3 and Section E in the appendix] experiments that show the empirical contribution of our suggested methods for real images (novel and reference), synthetic data, and real-world data. We also propose choice clustering, which by combining clustering algorithms yields better performance than each one separately.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge