Provable Compressed Sensing with Generative Priors via Langevin Dynamics
Paper and Code
Feb 25, 2021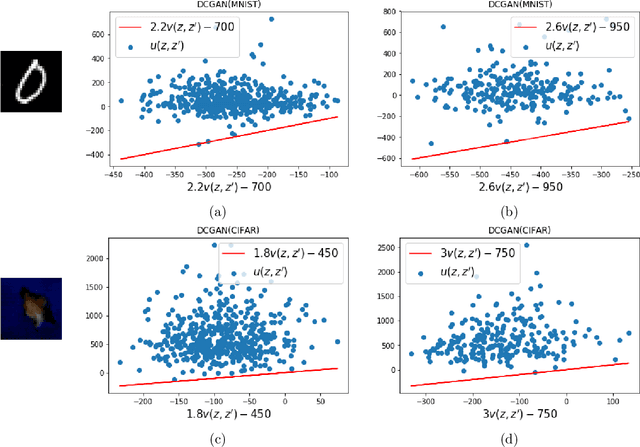


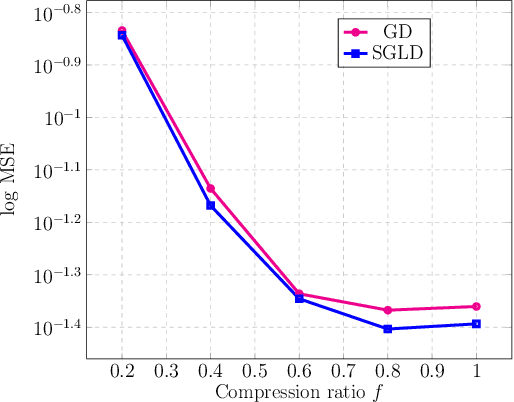
Deep generative models have emerged as a powerful class of priors for signals in various inverse problems such as compressed sensing, phase retrieval and super-resolution. Here, we assume an unknown signal to lie in the range of some pre-trained generative model. A popular approach for signal recovery is via gradient descent in the low-dimensional latent space. While gradient descent has achieved good empirical performance, its theoretical behavior is not well understood. In this paper, we introduce the use of stochastic gradient Langevin dynamics (SGLD) for compressed sensing with a generative prior. Under mild assumptions on the generative model, we prove the convergence of SGLD to the true signal. We also demonstrate competitive empirical performance to standard gradient descent.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge