Probabilistic Segmentation via Total Variation Regularization
Paper and Code
Nov 16, 2015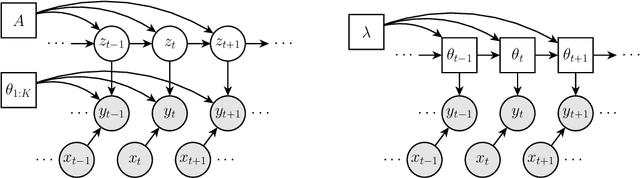

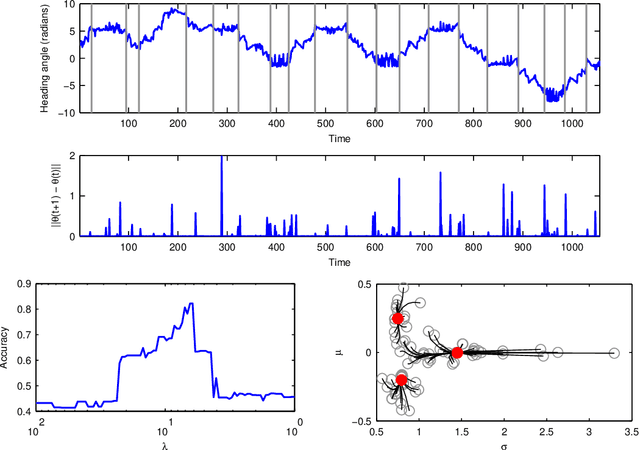
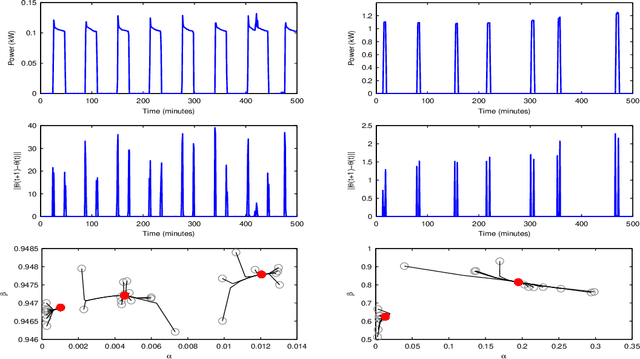
We present a convex approach to probabilistic segmentation and modeling of time series data. Our approach builds upon recent advances in multivariate total variation regularization, and seeks to learn a separate set of parameters for the distribution over the observations at each time point, but with an additional penalty that encourages the parameters to remain constant over time. We propose efficient optimization methods for solving the resulting (large) optimization problems, and a two-stage procedure for estimating recurring clusters under such models, based upon kernel density estimation. Finally, we show on a number of real-world segmentation tasks, the resulting methods often perform as well or better than existing latent variable models, while being substantially easier to train.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge