Probabilistic Inverse Optimal Transport
Paper and Code
Dec 17, 2021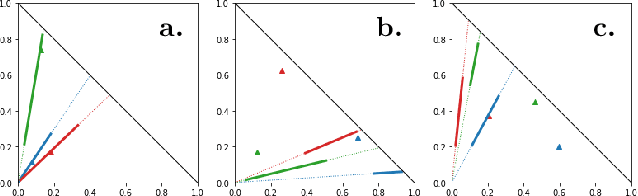
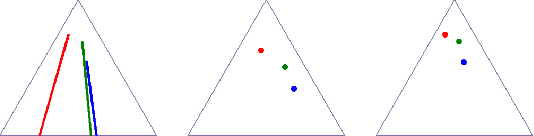
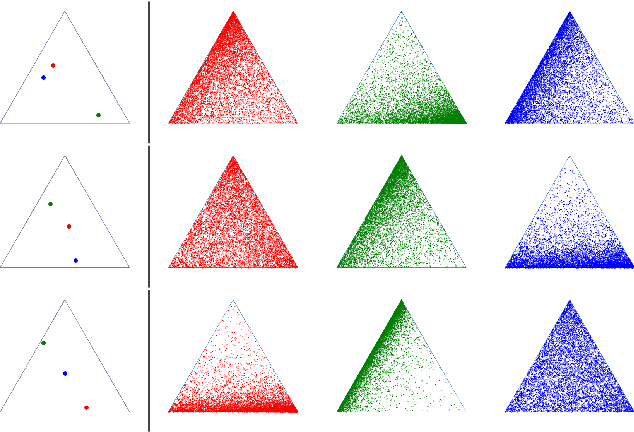
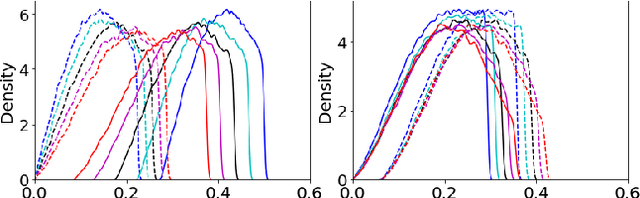
Optimal transport (OT) formalizes the problem of finding an optimal coupling between probability measures given a cost matrix. The inverse problem of inferring the cost given a coupling is Inverse Optimal Transport (IOT). IOT is less well understood than OT. We formalize and systematically analyze the properties of IOT using tools from the study of entropy-regularized OT. Theoretical contributions include characterization of the manifold of cross-ratio equivalent costs, the implications of model priors, and derivation of an MCMC sampler. Empirical contributions include visualizations of cross-ratio equivalent effect on basic examples and simulations validating theoretical results.
* 18 pages, 9 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge