Probabilistic Federated Learning of Neural Networks Incorporated with Global Posterior Information

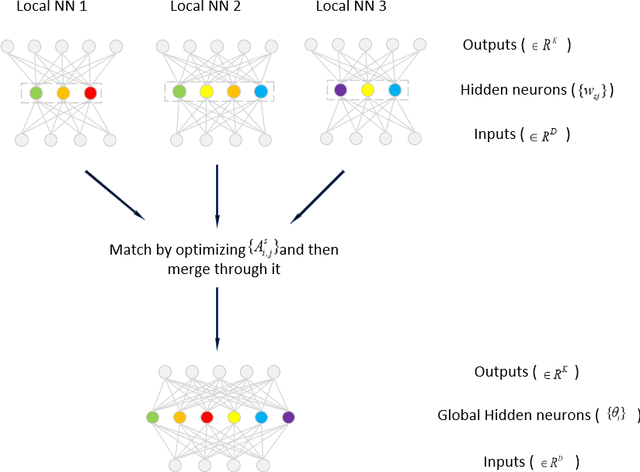
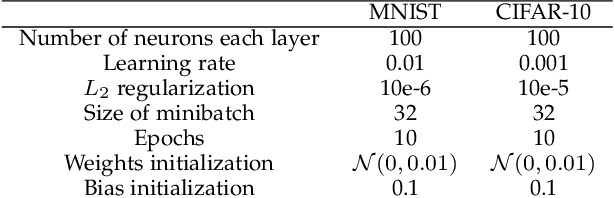
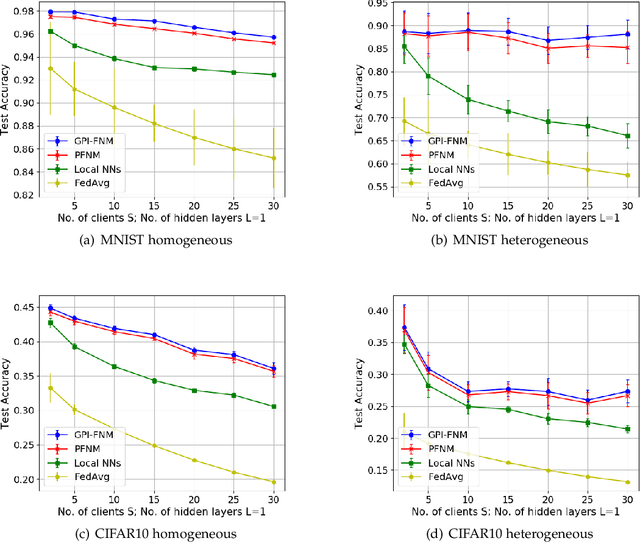
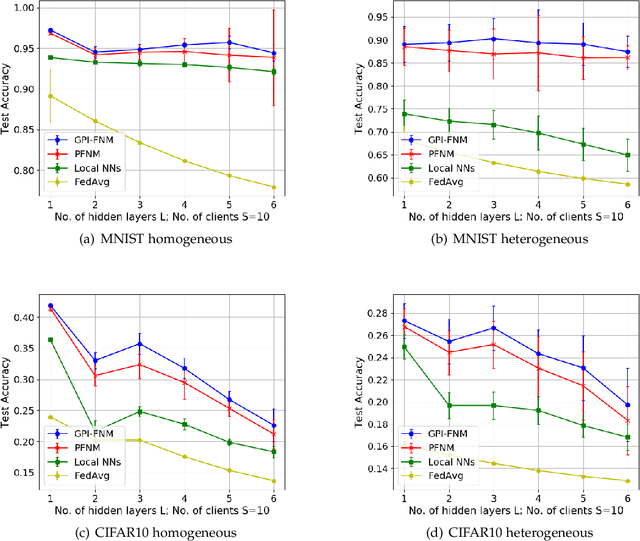
In federated learning, models trained on local clients are distilled into a global model. Due to the permutation invariance arises in neural networks, it is necessary to match the hidden neurons first when executing federated learning with neural networks. Through the Bayesian nonparametric framework, Probabilistic Federated Neural Matching (PFNM) matches and fuses local neural networks so as to adapt to varying global model size and the heterogeneity of the data. In this paper, we propose a new method which extends the PFNM with a Kullback-Leibler (KL) divergence over neural components product, in order to make inference exploiting posterior information in both local and global levels. We also show theoretically that The additional part can be seamlessly concatenated into the match-and-fuse progress. Through a series of simulations, it indicates that our new method outperforms popular state-of-the-art federated learning methods in both single communication round and additional communication rounds situation.