Private Convex Optimization via Exponential Mechanism
Paper and Code
Mar 01, 2022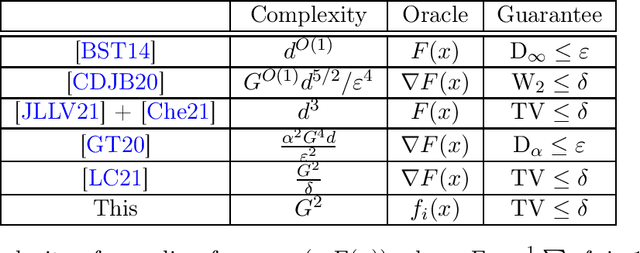
In this paper, we study private optimization problems for non-smooth convex functions $F(x)=\mathbb{E}_i f_i(x)$ on $\mathbb{R}^d$. We show that modifying the exponential mechanism by adding an $\ell_2^2$ regularizer to $F(x)$ and sampling from $\pi(x)\propto \exp(-k(F(x)+\mu\|x\|_2^2/2))$ recovers both the known optimal empirical risk and population loss under $(\epsilon,\delta)$-DP. Furthermore, we show how to implement this mechanism using $\widetilde{O}(n \min(d, n))$ queries to $f_i(x)$ for the DP-SCO where $n$ is the number of samples/users and $d$ is the ambient dimension. We also give a (nearly) matching lower bound $\widetilde{\Omega}(n \min(d, n))$ on the number of evaluation queries. Our results utilize the following tools that are of independent interest: (1) We prove Gaussian Differential Privacy (GDP) of the exponential mechanism if the loss function is strongly convex and the perturbation is Lipschitz. Our privacy bound is \emph{optimal} as it includes the privacy of Gaussian mechanism as a special case and is proved using the isoperimetric inequality for strongly log-concave measures. (2) We show how to sample from $\exp(-F(x)-\mu \|x\|^2_2/2)$ for $G$-Lipschitz $F$ with $\eta$ error in total variation (TV) distance using $\widetilde{O}((G^2/\mu) \log^2(d/\eta))$ unbiased queries to $F(x)$. This is the first sampler whose query complexity has \emph{polylogarithmic dependence} on both dimension $d$ and accuracy $\eta$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge