Privacy Amplification Via Bernoulli Sampling
Paper and Code
May 21, 2021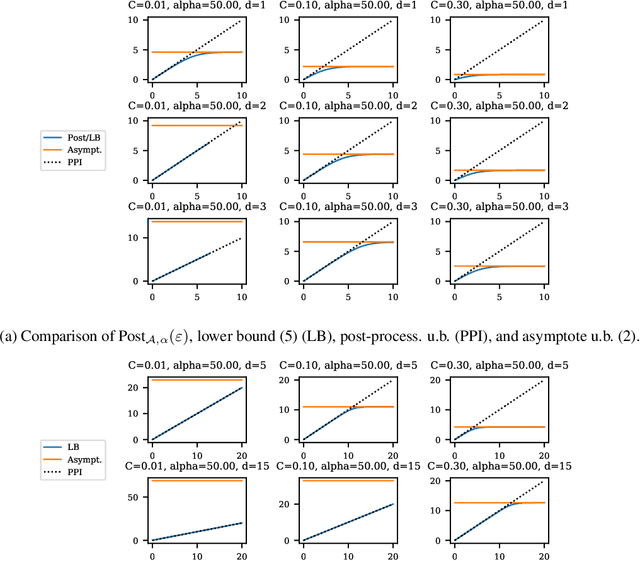
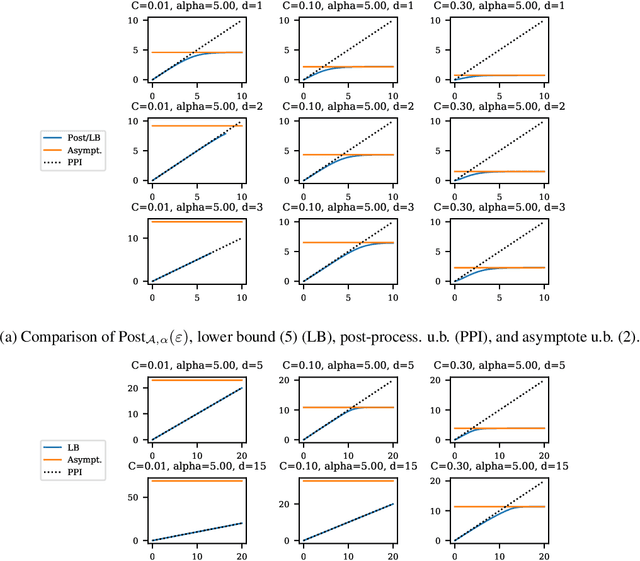
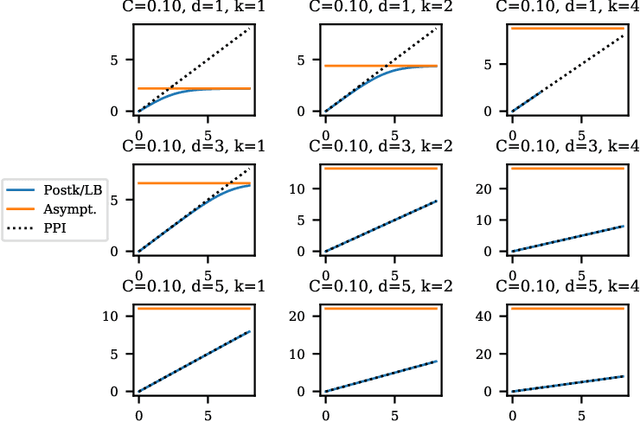
Balancing privacy and accuracy is a major challenge in designing differentially private machine learning algorithms. To improve this tradeoff, prior work has looked at privacy amplification methods which analyze how common training operations such as iteration and subsampling the data can lead to higher privacy. In this paper, we analyze privacy amplification properties of a new operation, sampling from the posterior, that is used in Bayesian inference. In particular, we look at Bernoulli sampling from a posterior that is described by a differentially private parameter. We provide an algorithm to compute the amplification factor in this setting, and establish upper and lower bounds on this factor. Finally, we look at what happens when we draw k posterior samples instead of one.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge