Predictive Data Calibration for Linear Correlation Significance Testing
Paper and Code
Aug 15, 2022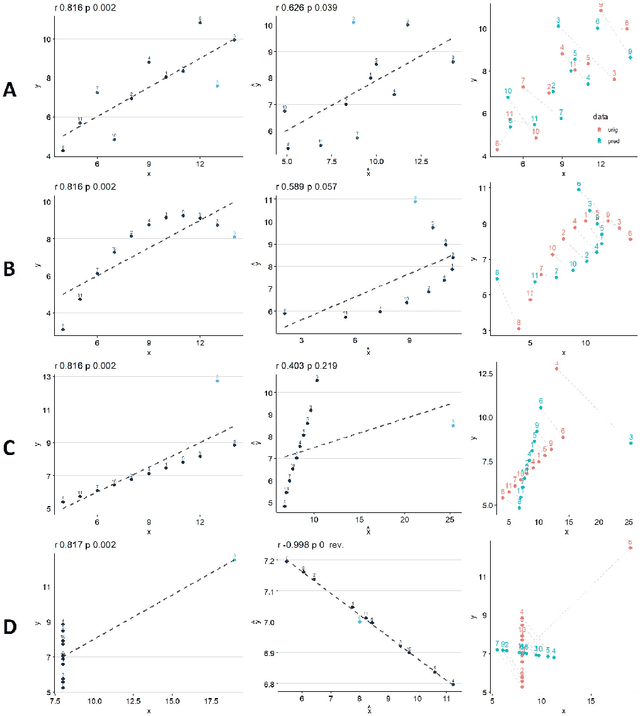
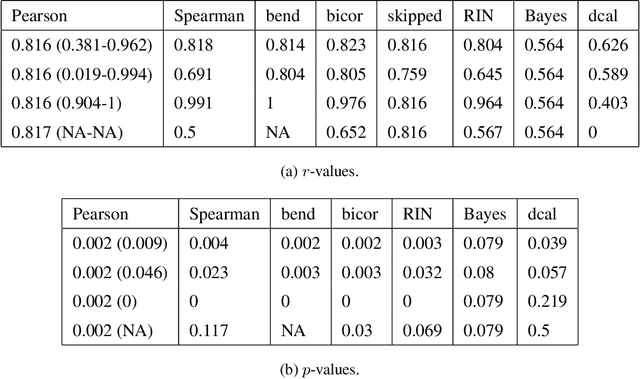
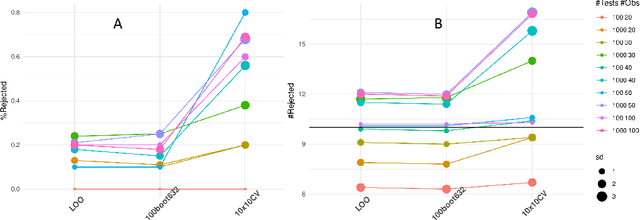
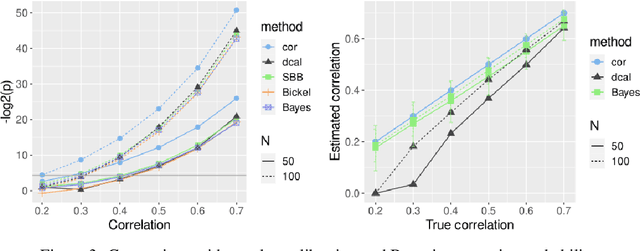
Inferring linear relationships lies at the heart of many empirical investigations. A measure of linear dependence should correctly evaluate the strength of the relationship as well as qualify whether it is meaningful for the population. Pearson's correlation coefficient (PCC), the \textit{de-facto} measure for bivariate relationships, is known to lack in both regards. The estimated strength $r$ maybe wrong due to limited sample size, and nonnormality of data. In the context of statistical significance testing, erroneous interpretation of a $p$-value as posterior probability leads to Type I errors -- a general issue with significance testing that extends to PCC. Such errors are exacerbated when testing multiple hypotheses simultaneously. To tackle these issues, we propose a machine-learning-based predictive data calibration method which essentially conditions the data samples on the expected linear relationship. Calculating PCC using calibrated data yields a calibrated $p$-value that can be interpreted as posterior probability together with a calibrated $r$ estimate, a desired outcome not provided by other methods. Furthermore, the ensuing independent interpretation of each test might eliminate the need for multiple testing correction. We provide empirical evidence favouring the proposed method using several simulations and application to real-world data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge