Prediction of System Evolution by Learning Machine

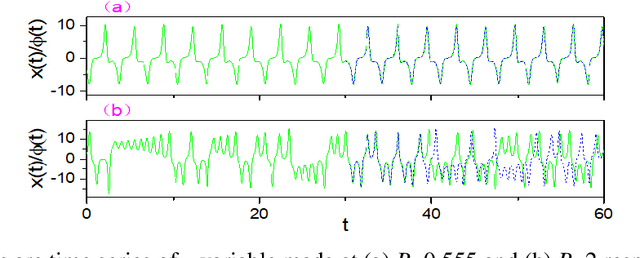
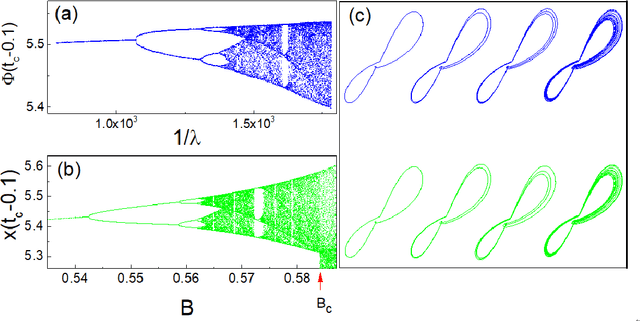
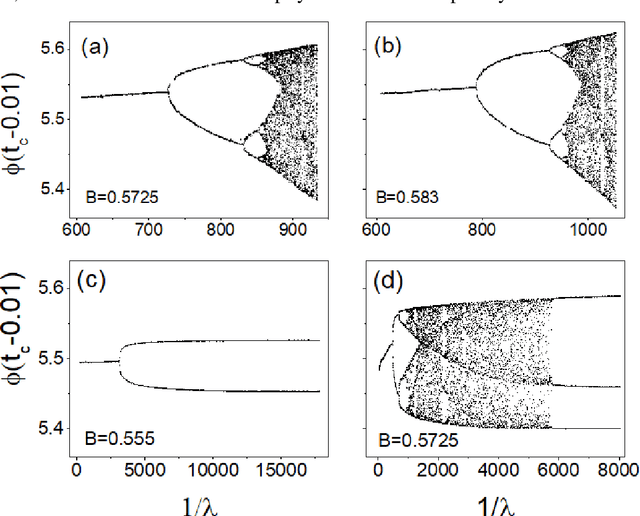
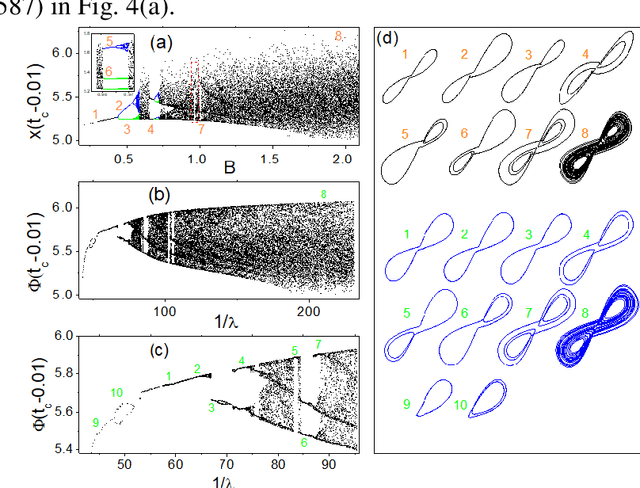
The orthodox approach for understanding a dynamical system is to establish its equation of motion, by which one can unveil its dynamical behavior at a given system parameter set, and reveal how the dynamic behavior evolves as the system parameters change. Here we show that this task can be fulfilled with a learning machine in a model-free way. We find that, based only on a segmental time series of a state variable recorded at present stage, the dynamics exhibited by the learning machine at different training stages can be mapped to the dynamics of the target system along a particular path in its parameter space following an appropriate training strategy that monotonously decreases the cost. This path is important, because along which the primary dynamical properties of the target system will emerge subsequently, in the simple-to-complex order, matching closely to the evolution of a natural system. A theoretical framework is proposed to explain the underlying mechanism. This revealed function of the learning machine opens up a novel way to probe the global dynamical properties of a black-box system without the equation of motion established artificially, and as such it might have huge potential applications. As an application example, this method is applied to infer what dynamical stages a variable star has experienced and how it will evolve in future by using the light curve observed presently.