Predicting the Likely Behaviors of Continuous Nonlinear Systems in Equilibrium
Paper and Code
Mar 27, 2013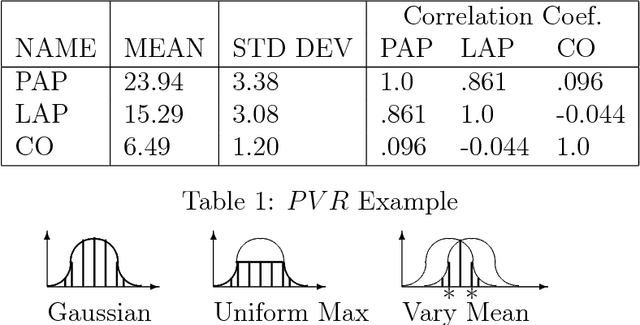
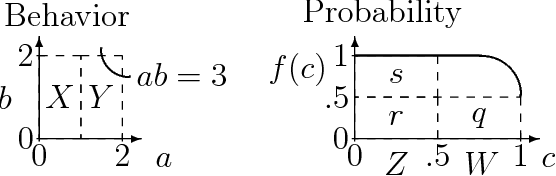

This paper introduces a method for predicting the likely behaviors of continuous nonlinear systems in equilibrium in which the input values can vary. The method uses a parameterized equation model and a lower bound on the input joint density to bound the likelihood that some behavior will occur, such as a state variable being inside a given numeric range. Using a bound on the density instead of the density itself is desirable because often the input density's parameters and shape are not exactly known. The new method is called SAB after its basic operations: split the input value space into smaller regions, and then bound those regions' possible behaviors and the probability of being in them. SAB finds rough bounds at first, and then refines them as more time is given. In contrast to other researchers' methods, SAB can (1) find all the possible system behaviors, and indicate how likely they are, (2) does not approximate the distribution of possible outcomes without some measure of the error magnitude, (3) does not use discretized variable values, which limit the events one can find probability bounds for, (4) can handle density bounds, and (5) can handle such criteria as two state variables both being inside a numeric range.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge