Predictability of Performance in Communication Networks Under Markovian Dynamics
Paper and Code
Aug 26, 2024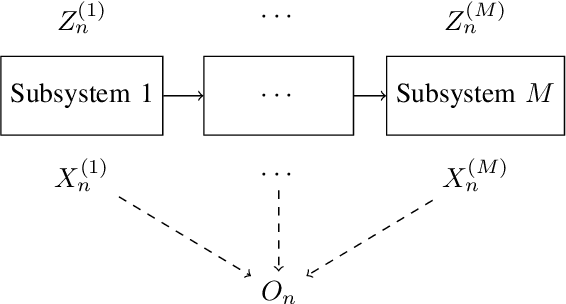
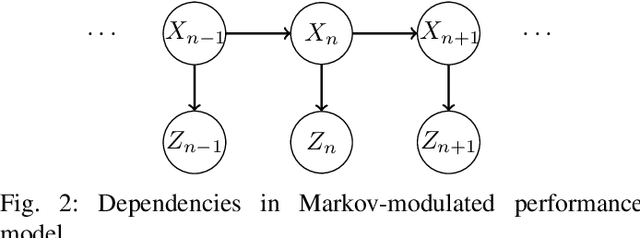
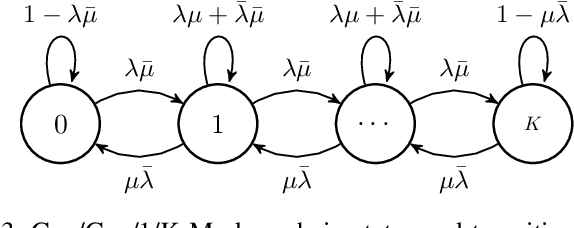
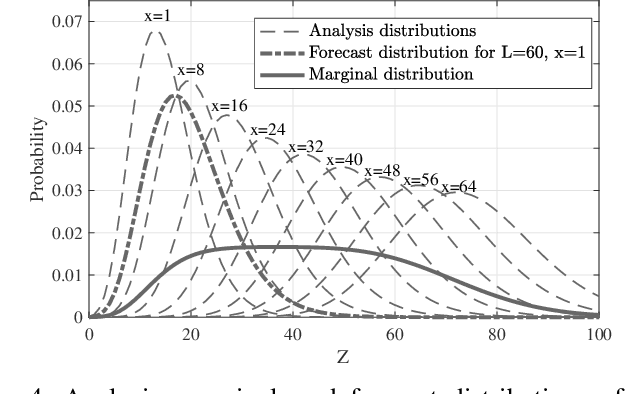
With the emergence of time-critical applications in modern communication networks, there is a growing demand for proactive network adaptation and quality of service (QoS) prediction. However, a fundamental question remains largely unexplored: how can we quantify and achieve more predictable communication systems in terms of performance? To address this gap, this paper introduces a theoretical framework for defining and analyzing predictability in communication systems, with a focus on the impact of observations for performance forecasting. We establish a mathematical definition of predictability based on the total variation distance between forecast and marginal performance distributions. A system is deemed unpredictable when the forecast distribution, providing the most comprehensive characterization of future states using all accessible information, is indistinguishable from the marginal distribution, which depicts the system's behavior without any observational input. This framework is applied to multi-hop systems under Markovian conditions, with a detailed analysis of Geo/Geo/1 queuing models in both single-hop and multi-hop scenarios. We derive exact and approximate expressions for predictability in these systems, as well as upper bounds based on spectral analysis of the underlying Markov chains. Our results have implications for the design of efficient monitoring and prediction mechanisms in future communication networks aiming to provide deterministic services.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge