Power of human-algorithm collaboration in solving combinatorial optimization problems
Paper and Code
Jul 25, 2021
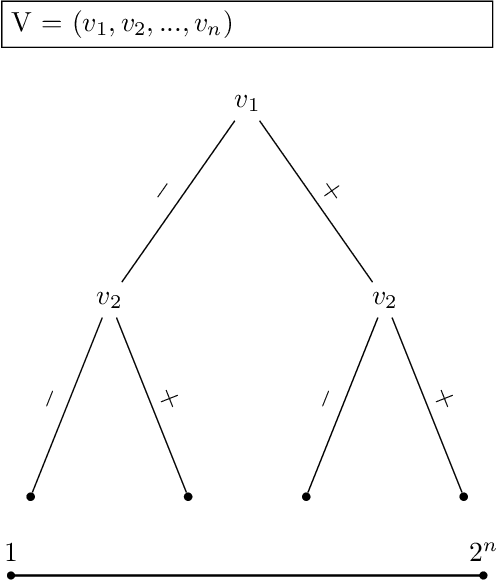
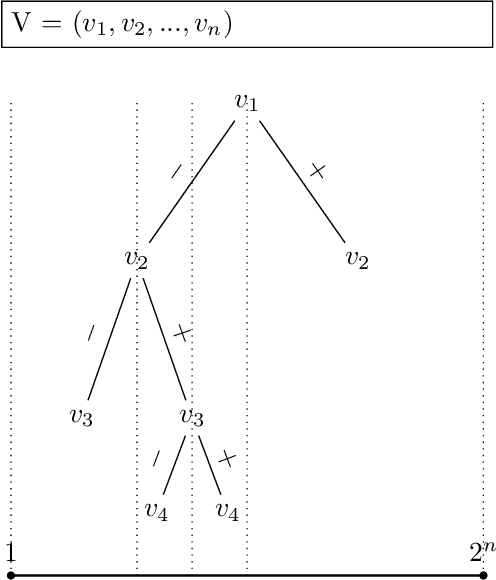
Many combinatorial optimization problems are often considered intractable to solve exactly or by approximation. An example of such problem is maximum clique which -- under standard assumptions in complexity theory -- cannot be solved in sub-exponential time or be approximated within polynomial factor efficiently. We show that if a polynomial time algorithm can query informative Gaussian priors from an expert $poly(n)$ times, then a class of combinatorial optimization problems can be solved efficiently in expectation up to a multiplicative factor $\epsilon$ where $\epsilon$ is arbitrary constant. While our proposed methods are merely theoretical, they cast new light on how to approach solving these problems that have been usually considered intractable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge