Power Normalizations in Fine-grained Image, Few-shot Image and Graph Classification
Paper and Code
Dec 27, 2020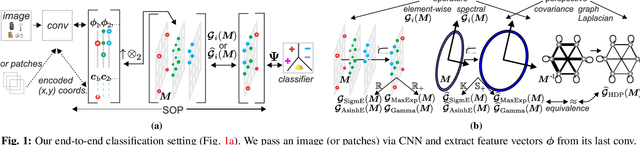
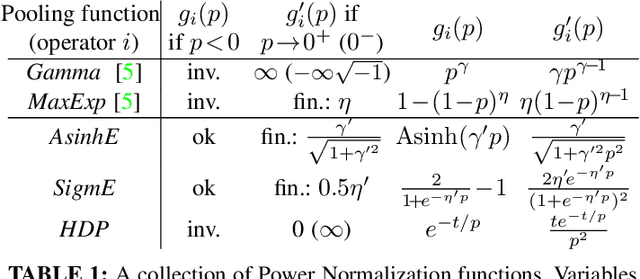
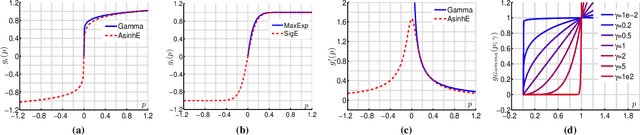

Power Normalizations (PN) are useful non-linear operators which tackle feature imbalances in classification problems. We study PNs in the deep learning setup via a novel PN layer pooling feature maps. Our layer combines the feature vectors and their respective spatial locations in the feature maps produced by the last convolutional layer of CNN into a positive definite matrix with second-order statistics to which PN operators are applied, forming so-called Second-order Pooling (SOP). As the main goal of this paper is to study Power Normalizations, we investigate the role and meaning of MaxExp and Gamma, two popular PN functions. To this end, we provide probabilistic interpretations of such element-wise operators and discover surrogates with well-behaved derivatives for end-to-end training. Furthermore, we look at the spectral applicability of MaxExp and Gamma by studying Spectral Power Normalizations (SPN). We show that SPN on the autocorrelation/covariance matrix and the Heat Diffusion Process (HDP) on a graph Laplacian matrix are closely related, thus sharing their properties. Such a finding leads us to the culmination of our work, a fast spectral MaxExp which is a variant of HDP for covariances/autocorrelation matrices. We evaluate our ideas on fine-grained recognition, scene recognition, and material classification, as well as in few-shot learning and graph classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge