PolyLUT: Learning Piecewise Polynomials for Ultra-Low Latency FPGA LUT-based Inference

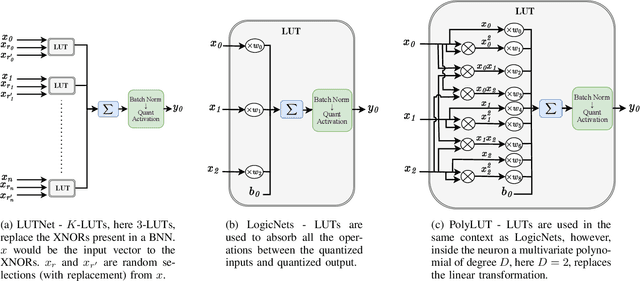
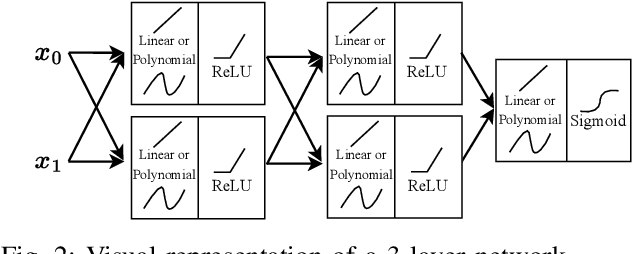
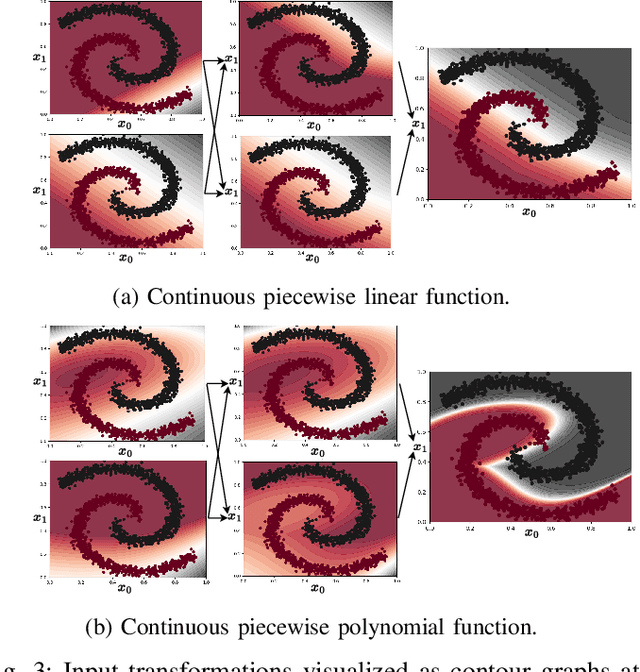
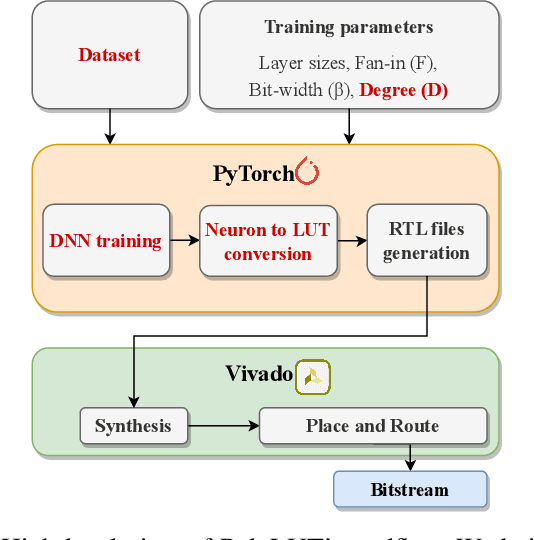
Field-programmable gate arrays (FPGAs) are widely used to implement deep learning inference. Standard deep neural network inference involves the computation of interleaved linear maps and nonlinear activation functions. Prior work for ultra-low latency implementations has hardcoded the combination of linear maps and nonlinear activations inside FPGA lookup tables (LUTs). Our work is motivated by the idea that the LUTs in an FPGA can be used to implement a much greater variety of functions than this. In this paper, we propose a novel approach to training neural networks for FPGA deployment using multivariate polynomials as the basic building block. Our method takes advantage of the flexibility offered by the soft logic, hiding the polynomial evaluation inside the LUTs with zero overhead. We show that by using polynomial building blocks, we can achieve the same accuracy using considerably fewer layers of soft logic than by using linear functions, leading to significant latency and area improvements. We demonstrate the effectiveness of this approach in three tasks: network intrusion detection, jet identification at the CERN Large Hadron Collider, and handwritten digit recognition using the MNIST dataset.