Poly-time universality and limitations of deep learning
Paper and Code
Jan 07, 2020
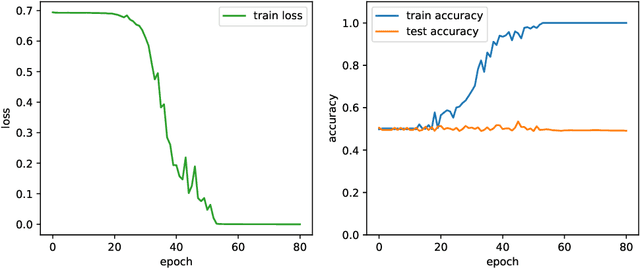
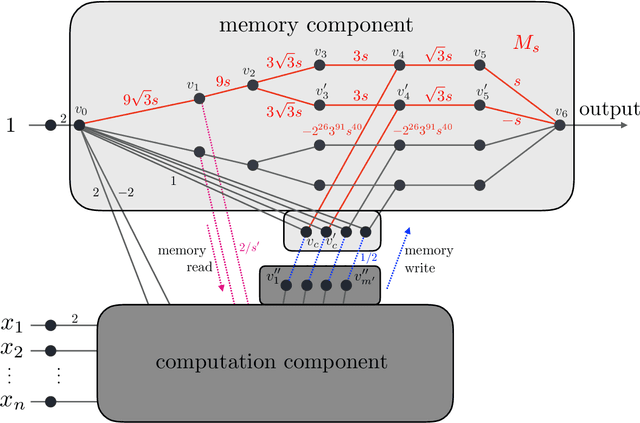
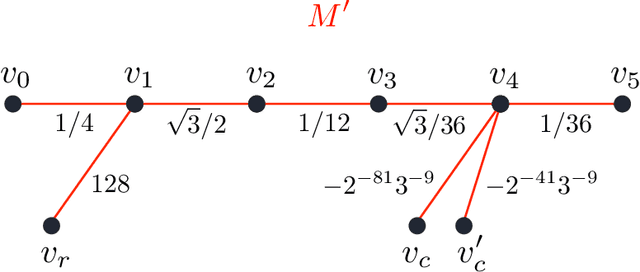
The goal of this paper is to characterize function distributions that deep learning can or cannot learn in poly-time. A universality result is proved for SGD-based deep learning and a non-universality result is proved for GD-based deep learning; this also gives a separation between SGD-based deep learning and statistical query algorithms: (1) {\it Deep learning with SGD is efficiently universal.} Any function distribution that can be learned from samples in poly-time can also be learned by a poly-size neural net trained with SGD on a poly-time initialization with poly-steps, poly-rate and possibly poly-noise. Therefore deep learning provides a universal learning paradigm: it was known that the approximation and estimation errors could be controlled with poly-size neural nets, using ERM that is NP-hard; this new result shows that the optimization error can also be controlled with SGD in poly-time. The picture changes for GD with large enough batches: (2) {\it Result (1) does not hold for GD:} Neural nets of poly-size trained with GD (full gradients or large enough batches) on any initialization with poly-steps, poly-range and at least poly-noise cannot learn any function distribution that has super-polynomial {\it cross-predictability,} where the cross-predictability gives a measure of ``average'' function correlation -- relations and distinctions to the statistical dimension are discussed. In particular, GD with these constraints can learn efficiently monomials of degree $k$ if and only if $k$ is constant. Thus (1) and (2) point to an interesting contrast: SGD is universal even with some poly-noise while full GD or SQ algorithms are not (e.g., parities).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge