POC-SLT: Partial Object Completion with SDF Latent Transformers
Paper and Code
Nov 08, 2024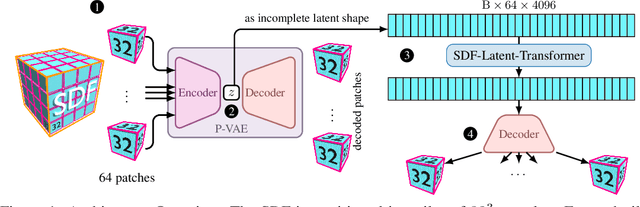

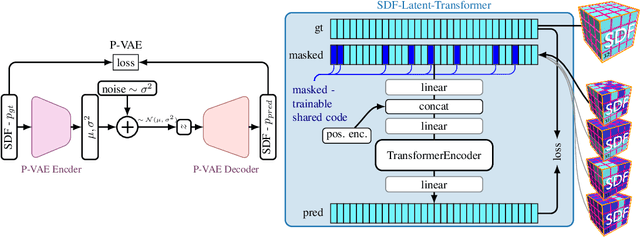
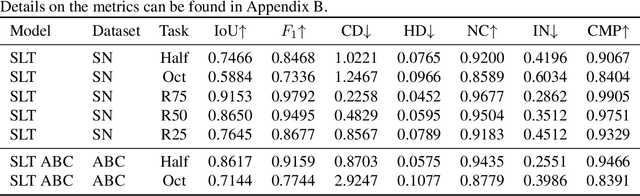
3D geometric shape completion hinges on representation learning and a deep understanding of geometric data. Without profound insights into the three-dimensional nature of the data, this task remains unattainable. Our work addresses this challenge of 3D shape completion given partial observations by proposing a transformer operating on the latent space representing Signed Distance Fields (SDFs). Instead of a monolithic volume, the SDF of an object is partitioned into smaller high-resolution patches leading to a sequence of latent codes. The approach relies on a smooth latent space encoding learned via a variational autoencoder (VAE), trained on millions of 3D patches. We employ an efficient masked autoencoder transformer to complete partial sequences into comprehensive shapes in latent space. Our approach is extensively evaluated on partial observations from ShapeNet and the ABC dataset where only fractions of the objects are given. The proposed POC-SLT architecture compares favorably with several baseline state-of-the-art methods, demonstrating a significant improvement in 3D shape completion, both qualitatively and quantitatively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge