Physics-informed UNets for Discovering Hidden Elasticity in Heterogeneous Materials
Paper and Code
Jun 07, 2023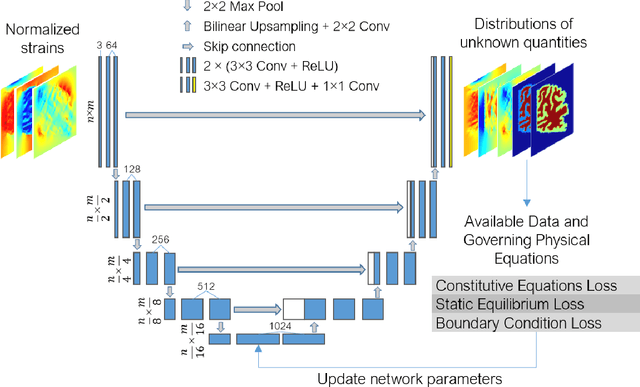
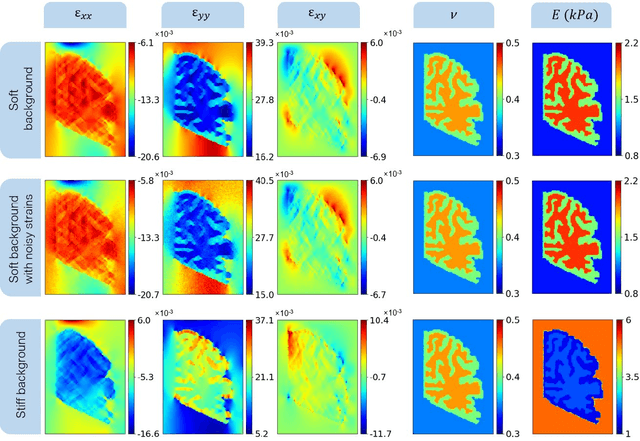
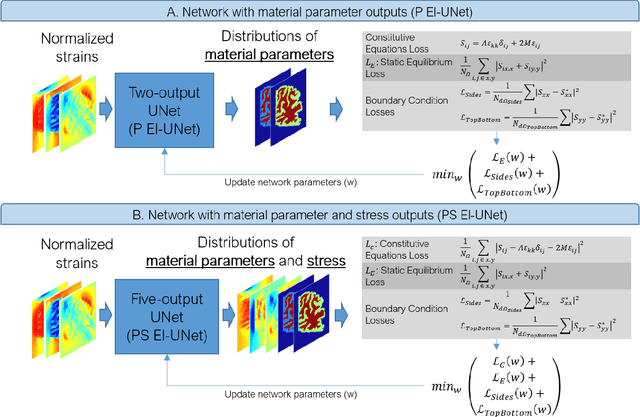
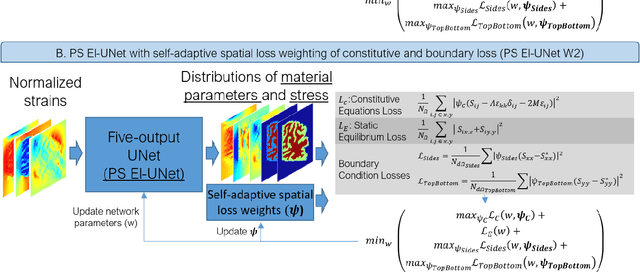
Soft biological tissues often have complex mechanical properties due to variation in structural components. In this paper, we develop a novel UNet-based neural network model for inversion in elasticity (El-UNet) to infer the spatial distributions of mechanical parameters from strain maps as input images, normal stress boundary conditions, and domain physics information. We show superior performance, both in terms of accuracy and computational cost, by El-UNet compared to fully-connected physics-informed neural networks in estimating unknown parameters and stress distributions for isotropic linear elasticity. We characterize different variations of El-UNet and propose a self-adaptive spatial loss weighting approach. To validate our inversion models, we performed various finite-element simulations of isotropic domains with heterogenous distributions of material parameters to generate synthetic data. El-UNet is faster and more accurate than the fully-connected physics-informed implementation in resolving the distribution of unknown fields. Among the tested models, the self-adaptive spatially weighted models had the most accurate reconstructions in equal computation times. The learned spatial weighting distribution visibly corresponded to regions that the unweighted models were resolving inaccurately. Our work demonstrates a computationally efficient inversion algorithm for elasticity imaging using convolutional neural networks and presents a potential fast framework for three-dimensional inverse elasticity problems that have proven unachievable through previously proposed methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge