Physics-enhanced Neural Networks in the Small Data Regime
Paper and Code
Nov 19, 2021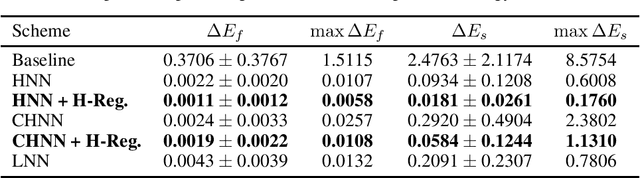

Identifying the dynamics of physical systems requires a machine learning model that can assimilate observational data, but also incorporate the laws of physics. Neural Networks based on physical principles such as the Hamiltonian or Lagrangian NNs have recently shown promising results in generating extrapolative predictions and accurately representing the system's dynamics. We show that by additionally considering the actual energy level as a regularization term during training and thus using physical information as inductive bias, the results can be further improved. Especially in the case where only small amounts of data are available, these improvements can significantly enhance the predictive capability. We apply the proposed regularization term to a Hamiltonian Neural Network (HNN) and Constrained Hamiltonian Neural Network (CHHN) for a single and double pendulum, generate predictions under unseen initial conditions and report significant gains in predictive accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge