Performance of Reconfigurable Intelligent Surfaces in the Presence of Generalized Gaussian Noise
Paper and Code
Nov 24, 2021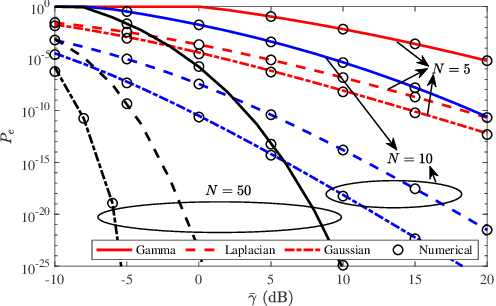
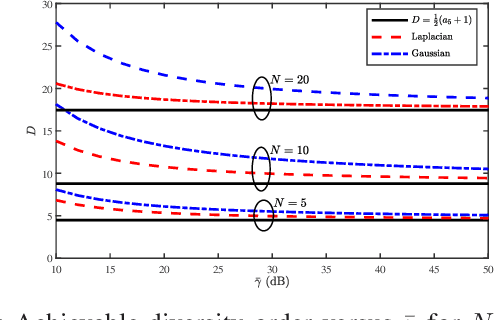
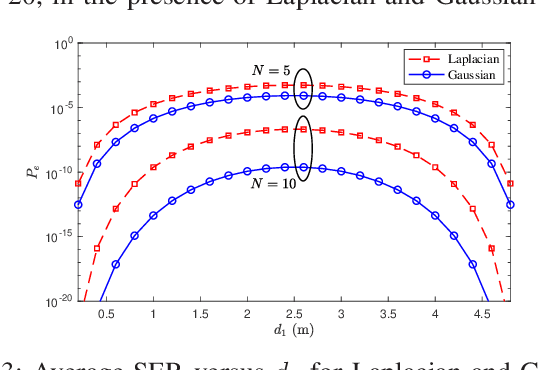

In this letter, we investigate the performance of reconfigurable intelligent surface (RIS)-assisted communications, under the assumption of generalized Gaussian noise (GGN), over Rayleigh fading channels. Specifically, we consider an RIS, equipped with $N$ reflecting elements, and derive a novel closed-form expression for the symbol error rate (SER) of arbitrary modulation schemes. The usefulness of the derived new expression is that it can be used to capture the SER performance in the presence of special additive noise distributions such as Gamma, Laplacian, and Gaussian noise. These special cases are also considered and their associated asymptotic SER expressions are derived, and then employed to quantify the achievable diversity order of the system. The theoretical framework is corroborated by numerical results, which reveal that the shaping parameter of the GGN ($\alpha$) has a negligible effect on the diversity order of RIS-assisted systems, particularly for large $\alpha$ values. Accordingly, the maximum achievable diversity order is determined by $N$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge