PCA-Boosted Autoencoders for Nonlinear Dimensionality Reduction in Low Data Regimes
Paper and Code
May 23, 2022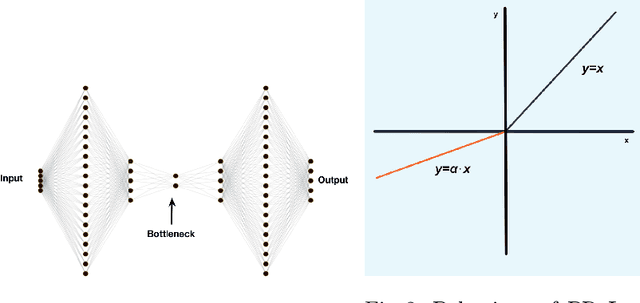
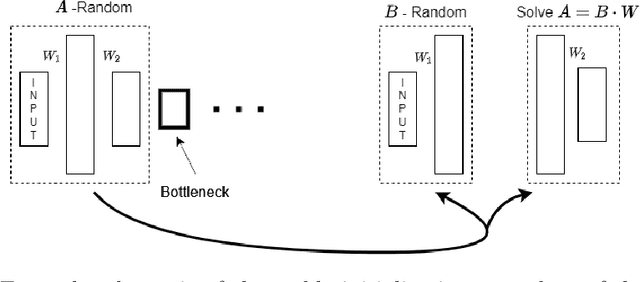
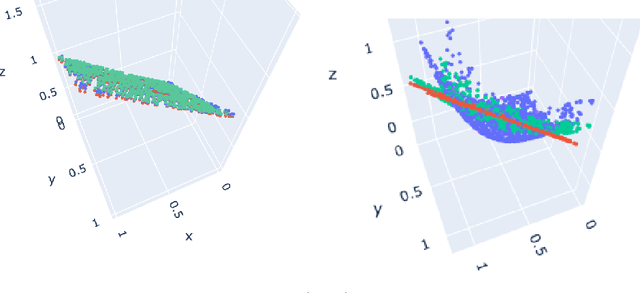
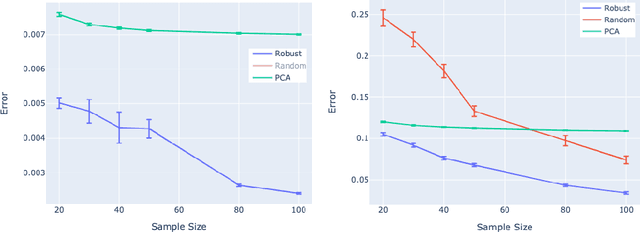
Autoencoders (AE) provide a useful method for nonlinear dimensionality reduction but are ill-suited for low data regimes. Conversely, Principal Component Analysis (PCA) is data-efficient but is limited to linear dimensionality reduction, posing a problem when data exhibits inherent nonlinearity. This presents a challenge in various scientific and engineering domains such as the nanophotonic component design, where data exhibits nonlinear features while being expensive to obtain due to costly real measurements or resource-consuming solutions of partial differential equations. To address this difficulty, we propose a technique that harnesses the best of both worlds: an autoencoder that leverages PCA to perform well on scarce nonlinear data. Specifically, we outline a numerically robust PCA-based initialization of AE, which, together with the parameterized ReLU activation function, allows the training process to start from an exact PCA solution and improve upon it. A synthetic example is presented first to study the effects of data nonlinearity and size on the performance of the proposed method. We then evaluate our method on several nanophotonic component design problems where obtaining useful data is expensive. To demonstrate universality, we also apply it to tasks in other scientific domains: a benchmark breast cancer dataset and a gene expression dataset. We show that our proposed approach is substantially better than both PCA and randomly initialized AE in the majority of low-data regime cases we consider, or at least is comparable to the best of either of the other two methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge