Partitioning sparse deep neural networks for scalable training and inference
Paper and Code
Apr 23, 2021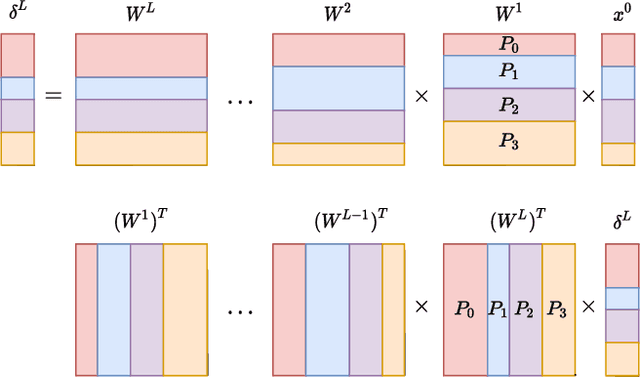

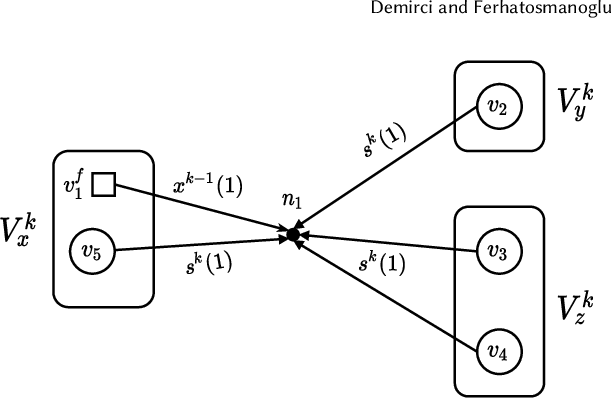
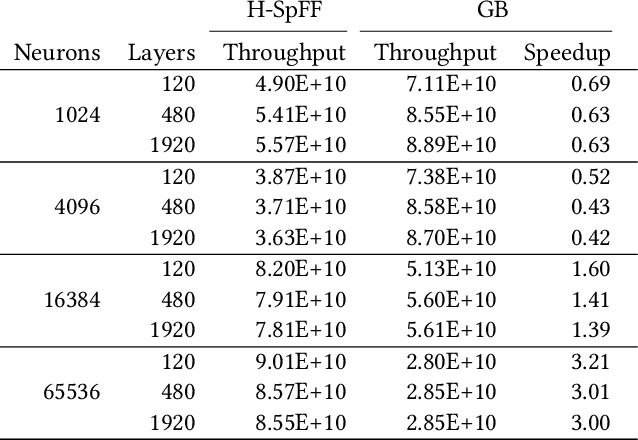
The state-of-the-art deep neural networks (DNNs) have significant computational and data management requirements. The size of both training data and models continue to increase. Sparsification and pruning methods are shown to be effective in removing a large fraction of connections in DNNs. The resulting sparse networks present unique challenges to further improve the computational efficiency of training and inference in deep learning. Both the feedforward (inference) and backpropagation steps in stochastic gradient descent (SGD) algorithm for training sparse DNNs involve consecutive sparse matrix-vector multiplications (SpMVs). We first introduce a distributed-memory parallel SpMV-based solution for the SGD algorithm to improve its scalability. The parallelization approach is based on row-wise partitioning of weight matrices that represent neuron connections between consecutive layers. We then propose a novel hypergraph model for partitioning weight matrices to reduce the total communication volume and ensure computational load-balance among processors. Experiments performed on sparse DNNs demonstrate that the proposed solution is highly efficient and scalable. By utilizing the proposed matrix partitioning scheme, the performance of our solution is further improved significantly.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge