Partially Observable Markov Decision Processes and Robotics

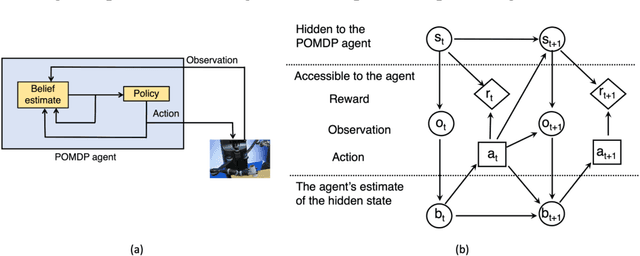
Planning under uncertainty is critical to robotics. The Partially Observable Markov Decision Process (POMDP) is a mathematical framework for such planning problems. It is powerful due to its careful quantification of the non-deterministic effects of actions and partial observability of the states. But precisely because of this, POMDP is notorious for its high computational complexity and deemed impractical for robotics. However, since early 2000, POMDPs solving capabilities have advanced tremendously, thanks to sampling-based approximate solvers. Although these solvers do not generate the optimal solution, they can compute good POMDP solutions that significantly improve the robustness of robotics systems within reasonable computational resources, thereby making POMDPs practical for many realistic robotics problems. This paper presents a review of POMDPs, emphasizing computational issues that have hindered its practicality in robotics and ideas in sampling-based solvers that have alleviated such difficulties, together with lessons learned from applying POMDPs to physical robots.