Parameterized Reinforcement Learning for Optical System Optimization
Paper and Code
Oct 09, 2020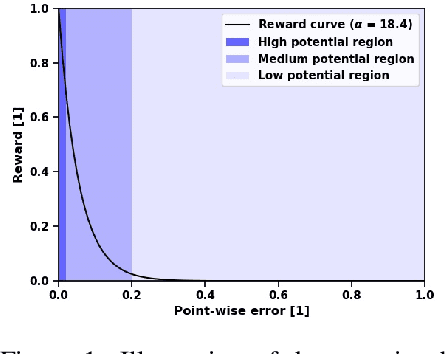

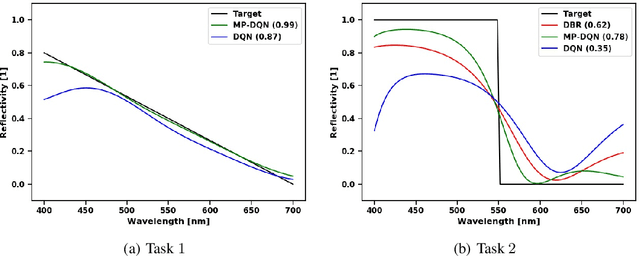
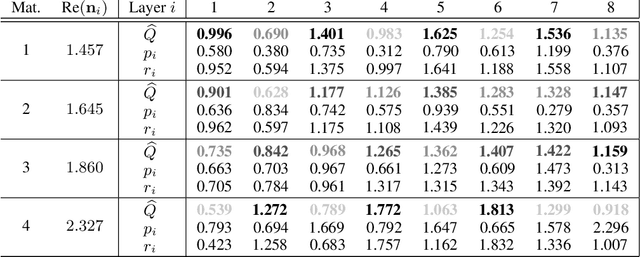
Designing a multi-layer optical system with designated optical characteristics is an inverse design problem in which the resulting design is determined by several discrete and continuous parameters. In particular, we consider three design parameters to describe a multi-layer stack: Each layer's dielectric material and thickness as well as the total number of layers. Such a combination of both, discrete and continuous parameters is a challenging optimization problem that often requires a computationally expensive search for an optimal system design. Hence, most methods merely determine the optimal thicknesses of the system's layers. To incorporate layer material and the total number of layers as well, we propose a method that considers the stacking of consecutive layers as parameterized actions in a Markov decision process. We propose an exponentially transformed reward signal that eases policy optimization and adapt a recent variant of Q-learning for inverse design optimization. We demonstrate that our method outperforms human experts and a naive reinforcement learning algorithm concerning the achieved optical characteristics. Moreover, the learned Q-values contain information about the optical properties of multi-layer optical systems, thereby allowing physical interpretation or what-if analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge