Parameter Identification for Digital Fabrication: A Gaussian Process Learning Approach
Paper and Code
Dec 20, 2020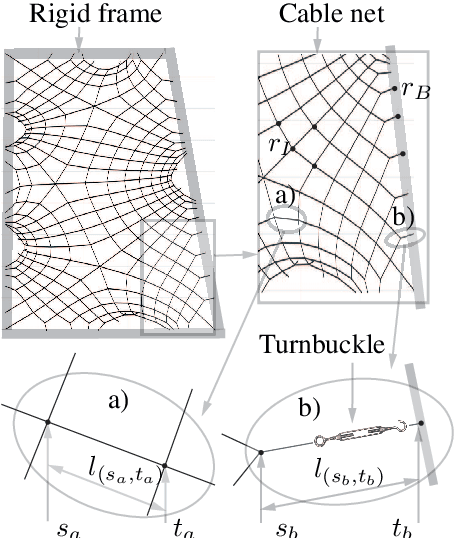
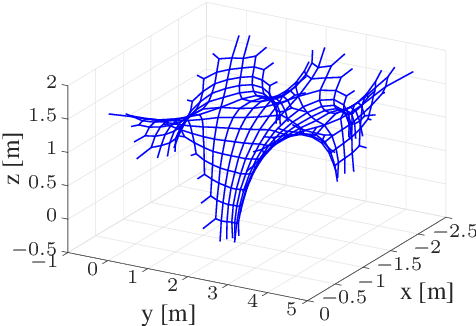
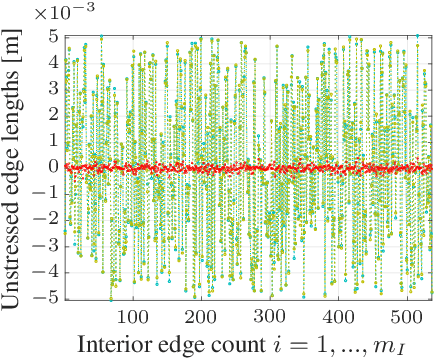
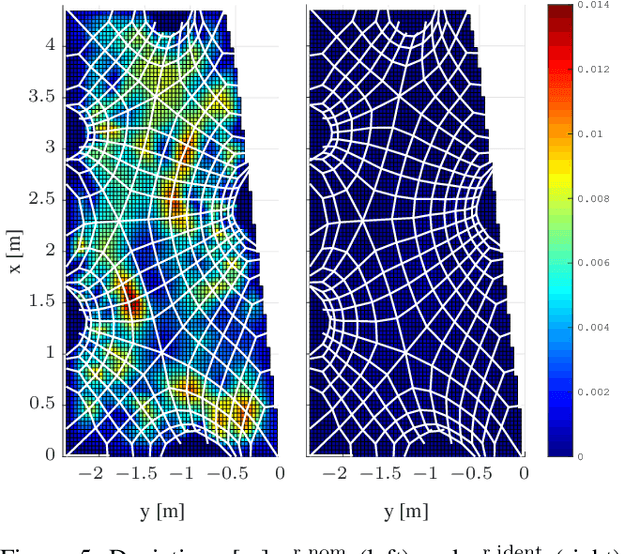
Tensioned cable nets can be used as supporting structures for the efficient construction of lightweight building elements, such as thin concrete shell structures. To guarantee important mechanical properties of the latter, the tolerances on deviations of the tensioned cable net geometry from the desired target form are very tight. Therefore, the form needs to be readjusted on the construction site. In order to employ model-based optimization techniques, the precise identification of important uncertain model parameters of the cable net system is required. This paper proposes the use of Gaussian process regression to learn the function that maps the cable net geometry to the uncertain parameters. In contrast to previously proposed methods, this approach requires only a single form measurement for the identification of the cable net model parameters. This is beneficial since measurements of the cable net form on the construction site are very expensive. For the training of the Gaussian processes, simulated data is efficiently computed via convex programming. The effectiveness of the proposed method and the impact of the precise identification of the parameters on the form of the cable net are demonstrated in numerical experiments on a quarter-scale prototype of a roof structure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge