Parallelizing Over Artificial Neural Network Training Runs with Multigrid
Paper and Code
Oct 01, 2017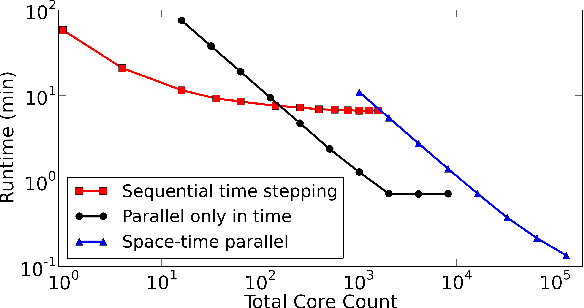



Artificial neural networks are a popular and effective machine learning technique. Great progress has been made parallelizing the expensive training phase of an individual network, leading to highly specialized pieces of hardware, many based on GPU-type architectures, and more concurrent algorithms such as synthetic gradients. However, the training phase continues to be a bottleneck, where the training data must be processed serially over thousands of individual training runs. This work considers a multigrid reduction in time (MGRIT) algorithm that is able to parallelize over the thousands of training runs and converge to the exact same solution as traditional training would provide. MGRIT was originally developed to provide parallelism for time evolution problems that serially step through a finite number of time-steps. This work recasts the training of a neural network similarly, treating neural network training as an evolution equation that evolves the network weights from one step to the next. Thus, this work concerns distributed computing approaches for neural networks, but is distinct from other approaches which seek to parallelize only over individual training runs. The work concludes with supporting numerical results for two model problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge