Pandemic model with data-driven phase detection, a study using COVID-19 data
Paper and Code
Oct 24, 2021
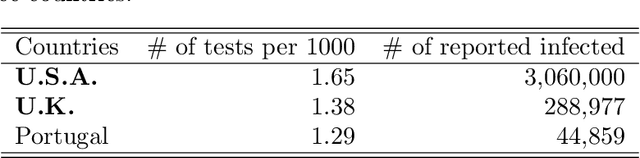
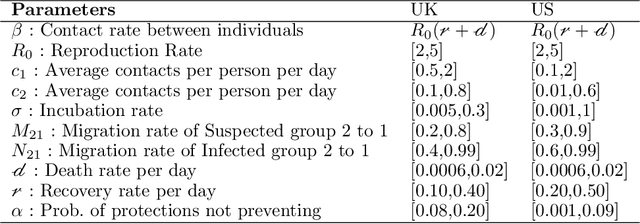

The recent COVID-19 pandemic has promoted vigorous scientific activity in an effort to understand, advice and control the pandemic. Data is now freely available at a staggering rate worldwide. Unfortunately, this unprecedented level of information contains a variety of data sources and formats, and the models do not always conform to the description of the data. Health officials have recognized the need for more accurate models that can adjust to sudden changes, such as produced by changes in behavior or social restrictions. In this work we formulate a model that fits a ``SIR''-type model concurrently with a statistical change detection test on the data. The result is a piece wise autonomous ordinary differential equation, whose parameters change at various points in time (automatically learned from the data). The main contributions of our model are: (a) providing interpretation of the parameters, (b) determining which parameters of the model are more important to produce changes in the spread of the disease, and (c) using data-driven discovery of sudden changes in the evolution of the pandemic. Together, these characteristics provide a new model that better describes the situation and thus, provides better quality of information for decision making.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge