Pairwise Adjusted Mutual Information
Paper and Code
Mar 23, 2021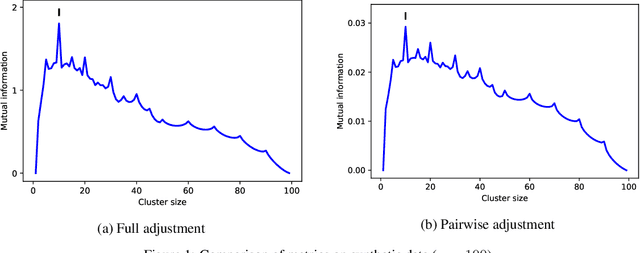
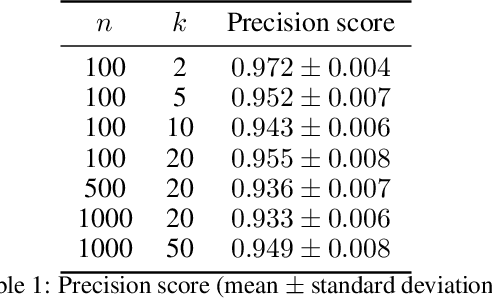
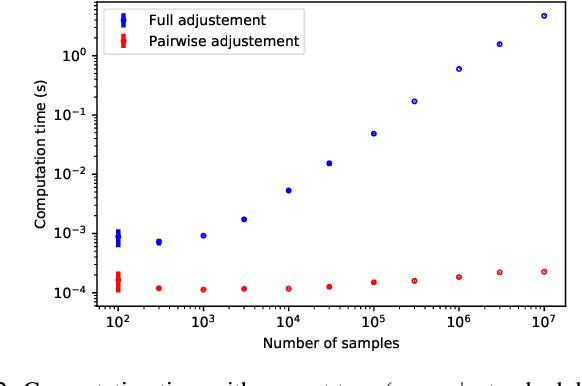
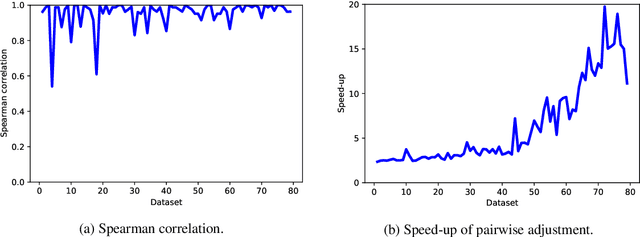
A well-known metric for quantifying the similarity between two clusterings is the adjusted mutual information. Compared to mutual information, a corrective term based on random permutations of the labels is introduced, preventing two clusterings being similar by chance. Unfortunately, this adjustment makes the metric computationally expensive. In this paper, we propose a novel adjustment based on {pairwise} label permutations instead of full label permutations. Specifically, we consider permutations where only two samples, selected uniformly at random, exchange their labels. We show that the corresponding adjusted metric, which can be expressed explicitly, behaves similarly to the standard adjusted mutual information for assessing the quality of a clustering, while having a much lower time complexity. Both metrics are compared in terms of quality and performance on experiments based on synthetic and real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge