Overcoming Challenges in Fixed Point Training of Deep Convolutional Networks
Paper and Code
Jul 08, 2016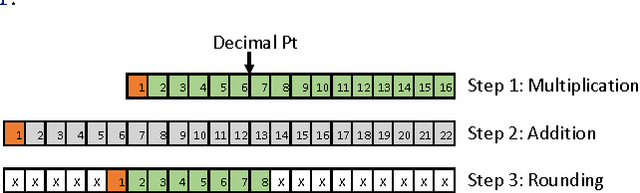
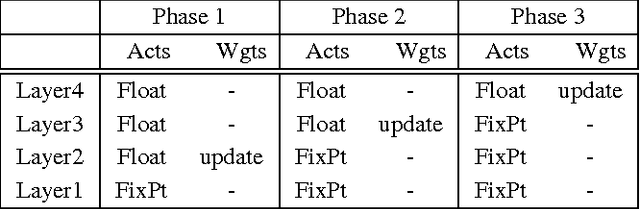
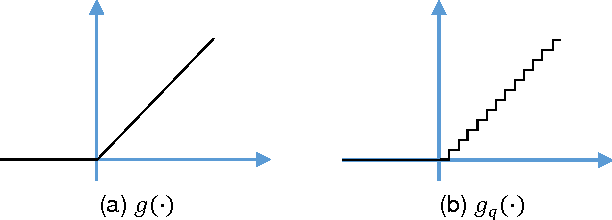

It is known that training deep neural networks, in particular, deep convolutional networks, with aggressively reduced numerical precision is challenging. The stochastic gradient descent algorithm becomes unstable in the presence of noisy gradient updates resulting from arithmetic with limited numeric precision. One of the well-accepted solutions facilitating the training of low precision fixed point networks is stochastic rounding. However, to the best of our knowledge, the source of the instability in training neural networks with noisy gradient updates has not been well investigated. This work is an attempt to draw a theoretical connection between low numerical precision and training algorithm stability. In doing so, we will also propose and verify through experiments methods that are able to improve the training performance of deep convolutional networks in fixed point.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge