Orthogonal Features-based EEG Signal Denoising using Fractionally Compressed AutoEncoder
Paper and Code
Feb 16, 2021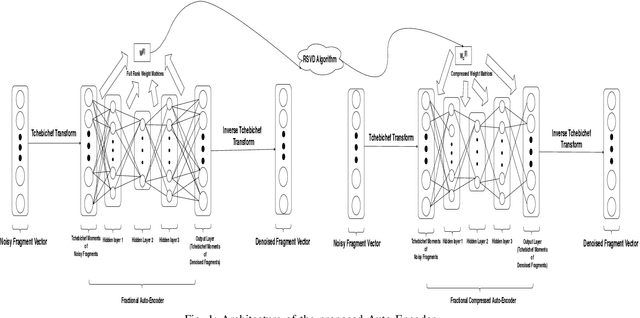
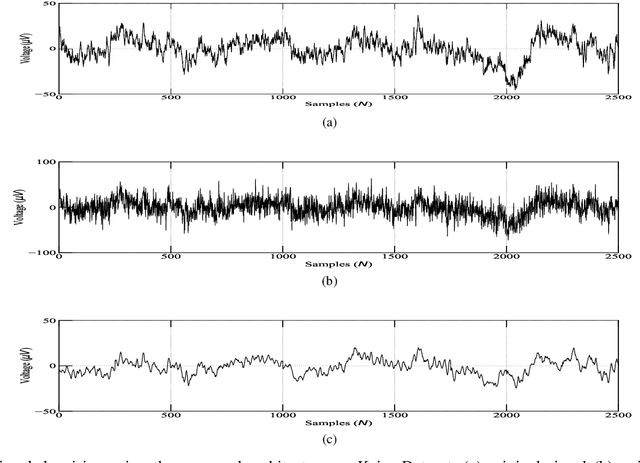
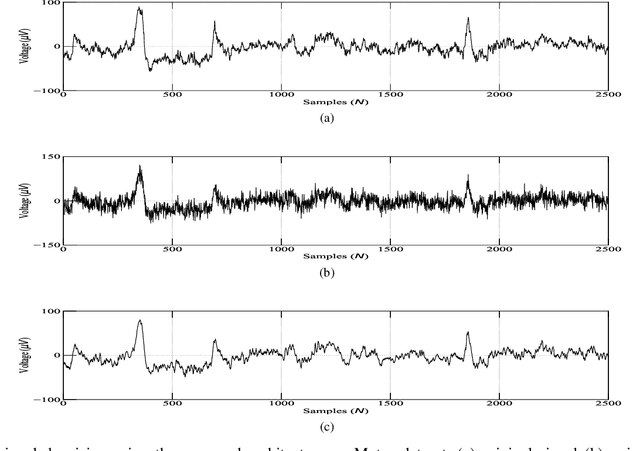
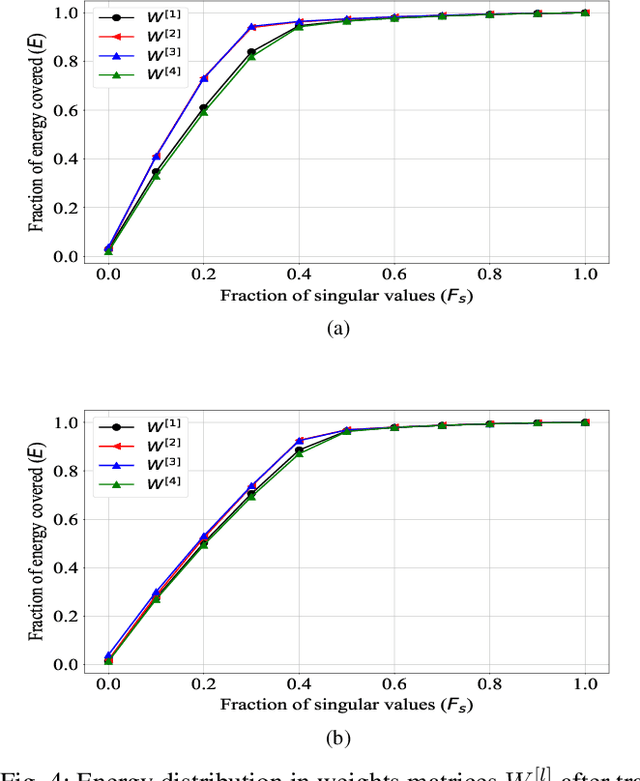
A fractional-based compressed auto-encoder architecture has been introduced to solve the problem of denoising electroencephalogram (EEG) signals. The architecture makes use of fractional calculus to calculate the gradients during the backpropagation process, as a result of which a new hyper-parameter in the form of fractional order ($\alpha$) has been introduced which can be tuned to get the best denoising performance. Additionally, to avoid substantial use of memory resources, the model makes use of orthogonal features in the form of Tchebichef moments as input. The orthogonal features have been used in achieving compression at the input stage. Considering the growing use of low energy devices, compression of neural networks becomes imperative. Here, the auto-encoder's weights are compressed using the randomized singular value decomposition (RSVD) algorithm during training while evaluation is performed using various compression ratios. The experimental results show that the proposed fractionally compressed architecture provides improved denoising results on the standard datasets when compared with the existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge