Optimizing Sparse Generalized Singular Vectors for Feature Selection in Proximal Support Vector Machines with Application to Breast and Ovarian Cancer Detection
Paper and Code
Oct 04, 2024
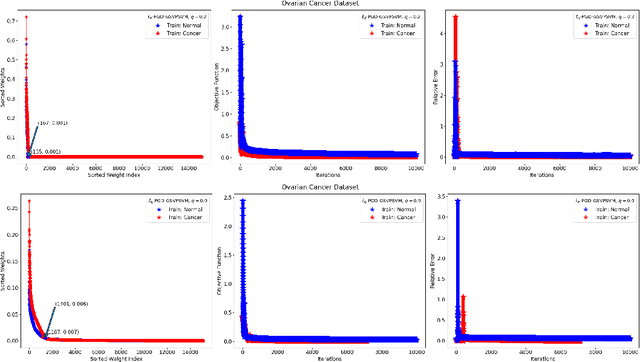
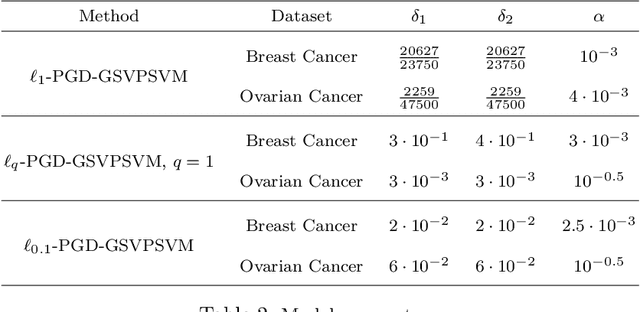
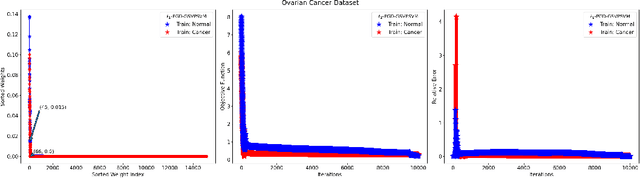
This paper presents approaches to compute sparse solutions of Generalized Singular Value Problem (GSVP). The GSVP is regularized by $\ell_1$-norm and $\ell_q$-penalty for $0<q<1$, resulting in the $\ell_1$-GSVP and $\ell_q$-GSVP formulations. The solutions of these problems are determined by applying the proximal gradient descent algorithm with a fixed step size. The inherent sparsity levels within the computed solutions are exploited for feature selection, and subsequently, binary classification with non-parallel Support Vector Machines (SVM). For our feature selection task, SVM is integrated into the $\ell_1$-GSVP and $\ell_q$-GSVP frameworks to derive the $\ell_1$-GSVPSVM and $\ell_q$-GSVPSVM variants. Machine learning applications to cancer detection are considered. We remarkably report near-to-perfect balanced accuracy across breast and ovarian cancer datasets using a few selected features.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge