Optimization via Low-rank Approximation for Community Detection in Networks
Paper and Code
May 10, 2015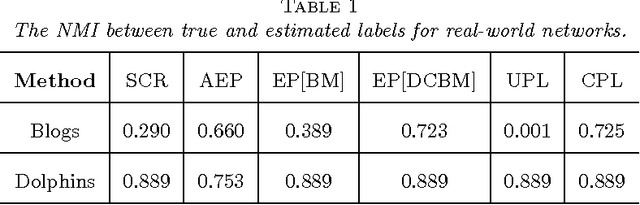
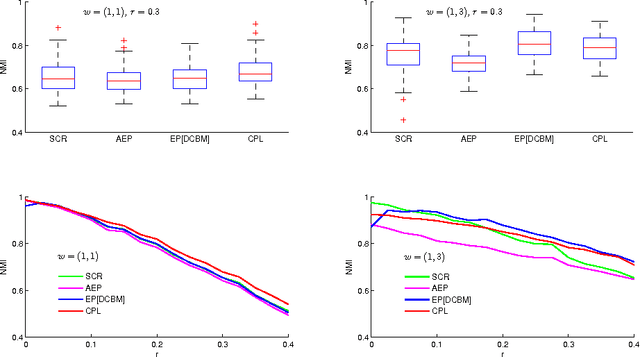
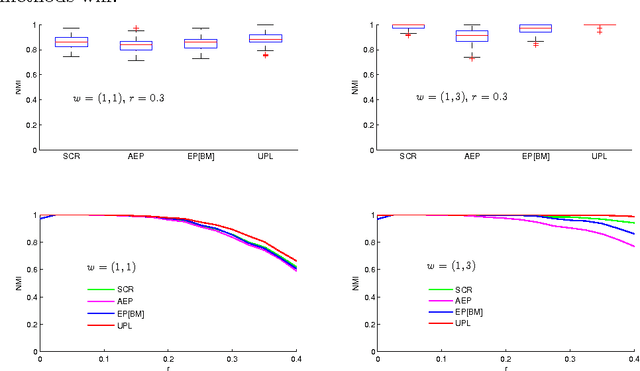
Community detection is one of the fundamental problems of network analysis, for which a number of methods have been proposed. Most model-based or criteria-based methods have to solve an optimization problem over a discrete set of labels to find communities, which is computationally infeasible. Some fast spectral algorithms have been proposed for specific methods or models, but only on a case-by-case basis. Here we propose a general approach for maximizing a function of a network adjacency matrix over discrete labels by projecting the set of labels onto a subspace approximating the leading eigenvectors of the expected adjacency matrix. This projection onto a low-dimensional space makes the feasible set of labels much smaller and the optimization problem much easier. We prove a general result about this method and show how to apply it to several previously proposed community detection criteria, establishing its consistency for label estimation in each case and demonstrating the fundamental connection between spectral properties of the network and various model-based approaches to community detection. Simulations and applications to real-world data are included to demonstrate our method performs well for multiple problems over a wide range of parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge