Optimization Under Uncertainty Using the Generalized Inverse Distribution Function
Paper and Code
Jul 17, 2014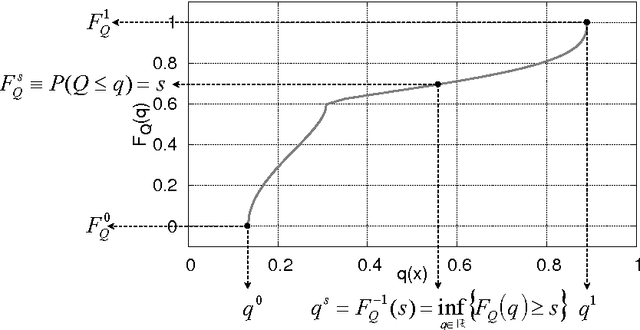


A framework for robust optimization under uncertainty based on the use of the generalized inverse distribution function (GIDF), also called quantile function, is here proposed. Compared to more classical approaches that rely on the usage of statistical moments as deterministic attributes that define the objectives of the optimization process, the inverse cumulative distribution function allows for the use of all the possible information available in the probabilistic domain. Furthermore, the use of a quantile based approach leads naturally to a multi-objective methodology which allows an a-posteriori selection of the candidate design based on risk/opportunity criteria defined by the designer. Finally, the error on the estimation of the objectives due to the resolution of the GIDF will be proven to be quantifiable
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge