Optimization of Mobile Robotic Relay Operation for Minimal Average Wait Time
Paper and Code
Aug 23, 2022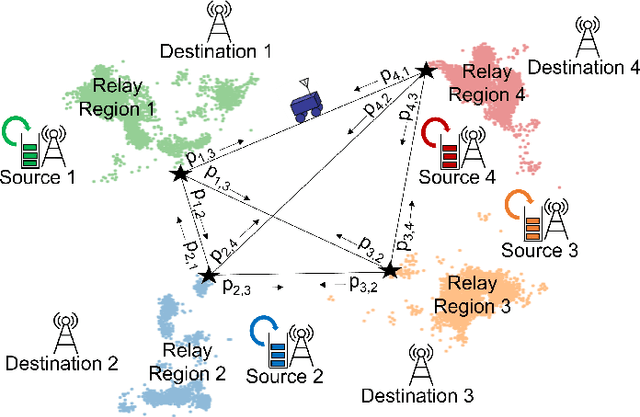

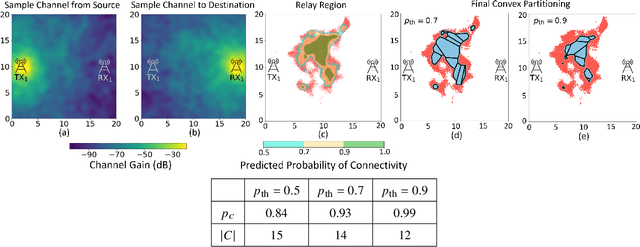
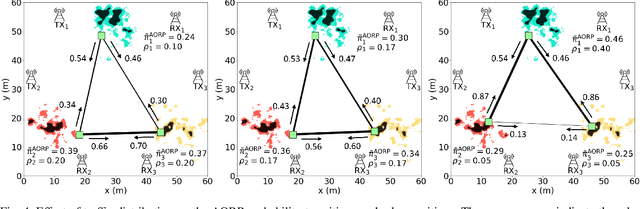
This paper considers trajectory planning for a mobile robot which persistently relays data between pairs of far-away communication nodes. Data accumulates stochastically at each source, and the robot must move to appropriate positions to enable data offload to the corresponding destination. The robot needs to minimize the average time that data waits at a source before being serviced. We are interested in finding optimal robotic routing policies consisting of 1) locations where the robot stops to relay (relay positions) and 2) conditional transition probabilities that determine the sequence in which the pairs are serviced. We first pose this problem as a non-convex problem that optimizes over both relay positions and transition probabilities. To find approximate solutions, we propose a novel algorithm which alternately optimizes relay positions and transition probabilities. For the former, we find efficient convex partitions of the non-convex relay regions, then formulate a mixed-integer second-order cone problem. For the latter, we find optimal transition probabilities via sequential least squares programming. We extensively analyze the proposed approach and mathematically characterize important system properties related to the robot's long-term energy consumption and service rate. Finally, through extensive simulation with real channel parameters, we verify the efficacy of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge