Optimization Based Motion Planning for Multi-Limbed Vertical Climbing Robots
Paper and Code
Sep 13, 2019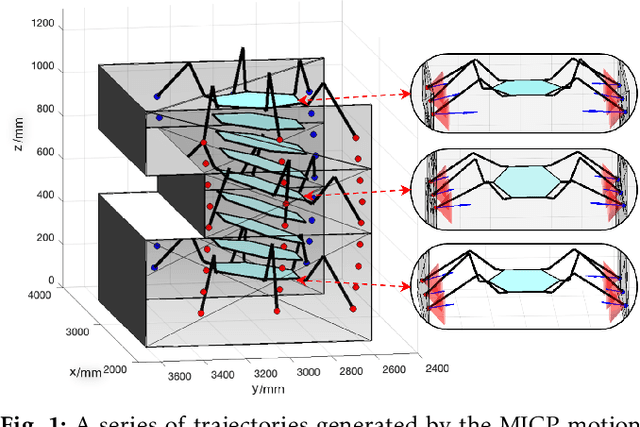
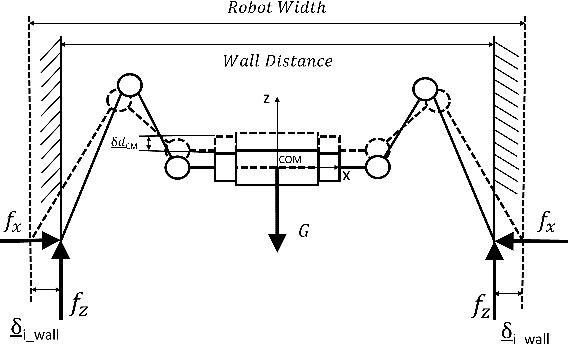
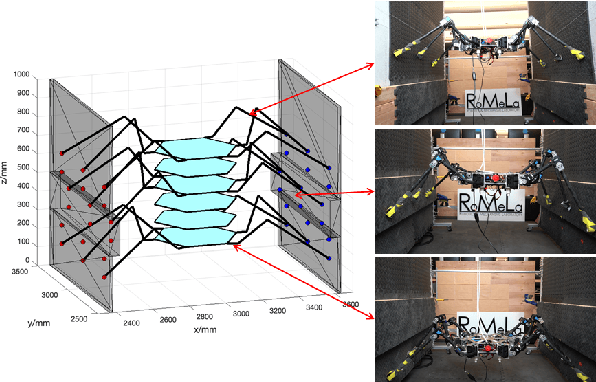
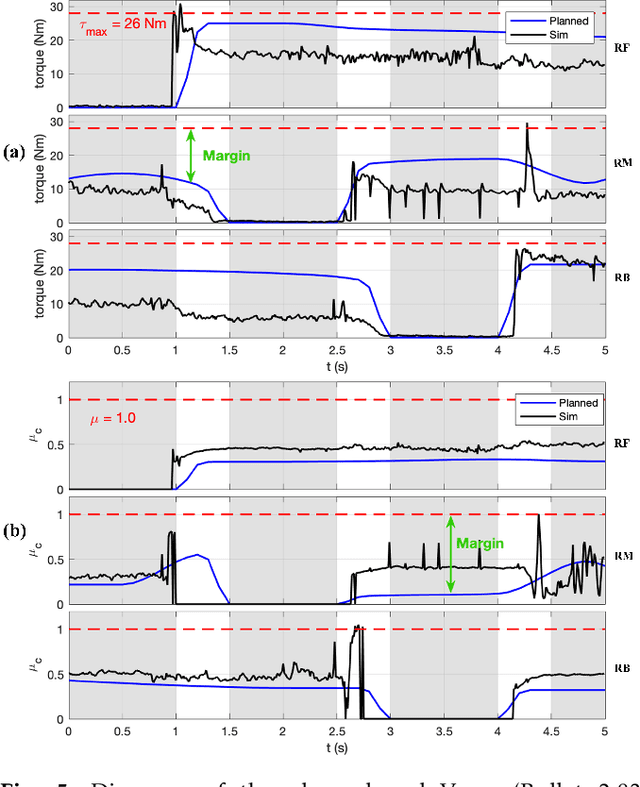
Motion planning trajectories for a multi-limbed robot to climb up walls requires a unique combination of constraints on torque, contact force, and posture. This paper focuses on motion planning for one particular setup wherein a six-legged robot braces itself between two vertical walls and climbs vertically with end effectors that only use friction. Instead of motion planning with a single nonlinear programming (NLP) solver, we decoupled the problem into two parts with distinct physical meaning: torso postures and contact forces. The first part can be formulated as either a mixed-integer convex programming (MICP) or NLP problem, while the second part is formulated as a series of standard convex optimization problems. Variants of the two wall climbing problem e.g., obstacle avoidance, uneven surfaces, and angled walls, help verify the proposed method in simulation and experimentation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge