Optimal transport for causal discovery

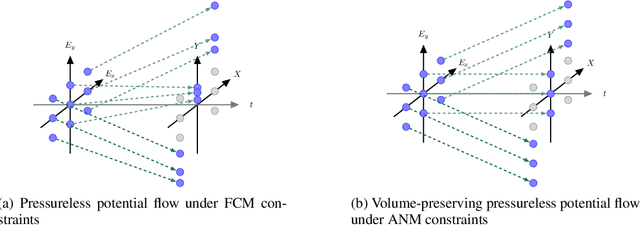
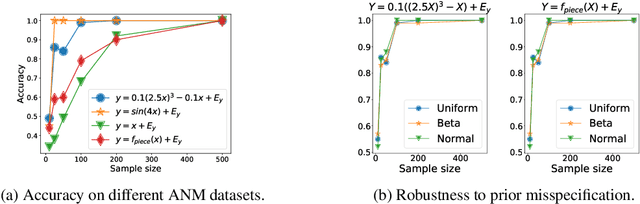
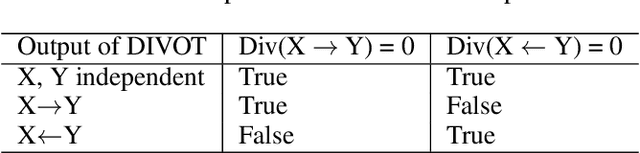
Approaches based on Functional Causal Models (FCMs) have been proposed to determine causal direction between two variables, by properly restricting model classes; however, their performance is sensitive to the model assumptions, which makes it difficult for practitioners to use. In this paper, we provide a novel dynamical-system view of FCMs and propose a new framework for identifying causal direction in the bivariate case. We first show the connection between FCMs and optimal transport, and then study optimal transport under the constraints of FCMs. Furthermore, by exploiting the dynamical interpretation of optimal transport under the FCM constraints, we determine the corresponding underlying dynamical process of the static cause-effect pair data under the least action principle. It provides a new dimension for describing static causal discovery tasks, while enjoying more freedom for modeling the quantitative causal influences. In particular, we show that Additive Noise Models (ANMs) correspond to volume-preserving pressureless flows. Consequently, based on their velocity field divergence, we introduce a criterion to determine causal direction. With this criterion, we propose a novel optimal transport-based algorithm for ANMs which is robust to the choice of models and extend it to post-noninear models. Our method demonstrated state-of-the-art results on both synthetic and causal discovery benchmark datasets.