Optimal training of finitely-sampled quantum reservoir computers for forecasting of chaotic dynamics
Paper and Code
Sep 02, 2024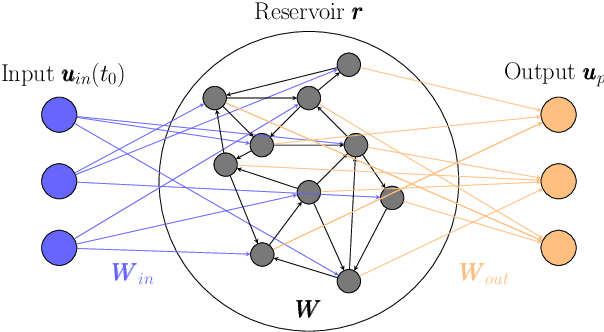
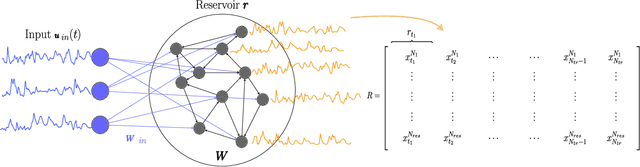
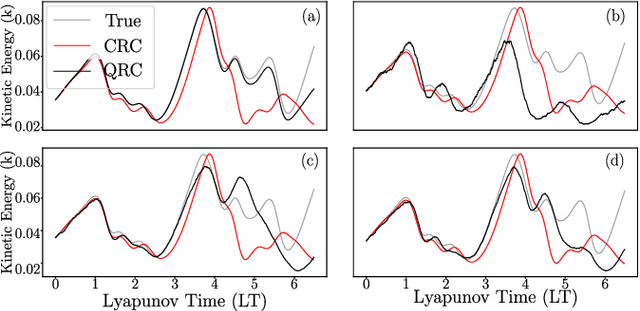
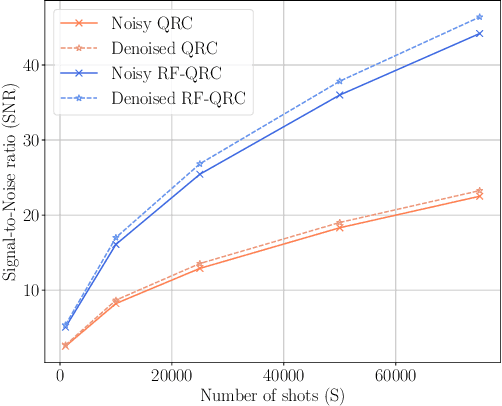
In the current Noisy Intermediate Scale Quantum (NISQ) era, the presence of noise deteriorates the performance of quantum computing algorithms. Quantum Reservoir Computing (QRC) is a type of Quantum Machine Learning algorithm, which, however, can benefit from different types of tuned noise. In this paper, we analyse the effect that finite-sampling noise has on the chaotic time-series prediction capabilities of QRC and Recurrence-free Quantum Reservoir Computing (RF-QRC). First, we show that, even without a recurrent loop, RF-QRC contains temporal information about previous reservoir states using leaky integrated neurons. This makes RF-QRC different from Quantum Extreme Learning Machines (QELM). Second, we show that finite sampling noise degrades the prediction capabilities of both QRC and RF-QRC while affecting QRC more due to the propagation of noise. Third, we optimize the training of the finite-sampled quantum reservoir computing framework using two methods: (a) Singular Value Decomposition (SVD) applied to the data matrix containing noisy reservoir activation states; and (b) data-filtering techniques to remove the high-frequencies from the noisy reservoir activation states. We show that denoising reservoir activation states improve the signal-to-noise ratios with smaller training loss. Finally, we demonstrate that the training and denoising of the noisy reservoir activation signals in RF-QRC are highly parallelizable on multiple Quantum Processing Units (QPUs) as compared to the QRC architecture with recurrent connections. The analyses are numerically showcased on prototypical chaotic dynamical systems with relevance to turbulence. This work opens opportunities for using quantum reservoir computing with finite samples for time-series forecasting on near-term quantum hardware.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge