Optimal Subsampling for Large Sample Logistic Regression
Paper and Code
Mar 07, 2018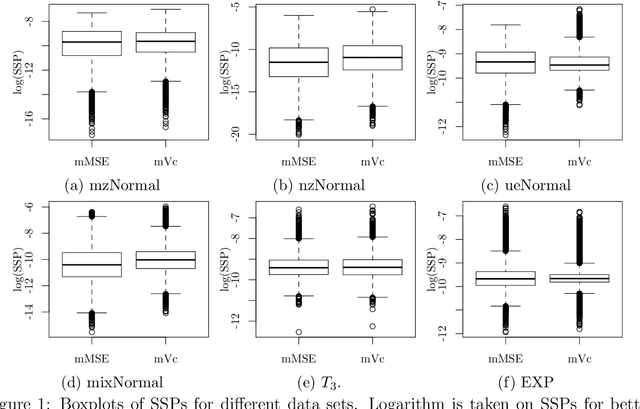

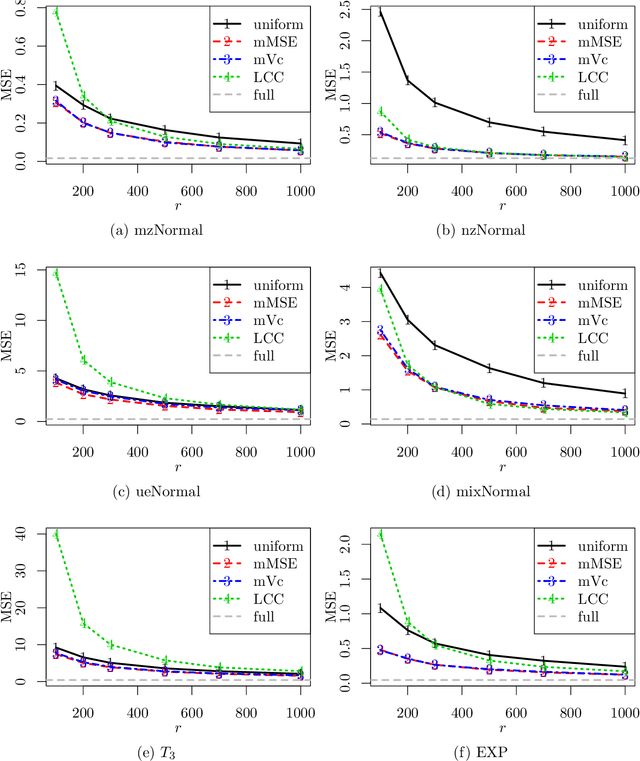
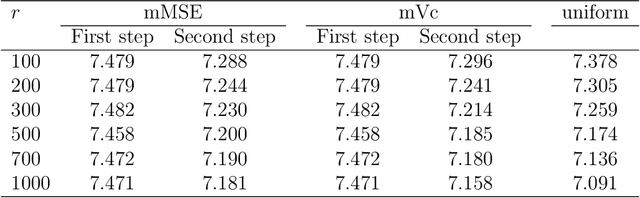
For massive data, the family of subsampling algorithms is popular to downsize the data volume and reduce computational burden. Existing studies focus on approximating the ordinary least squares estimate in linear regression, where statistical leverage scores are often used to define subsampling probabilities. In this paper, we propose fast subsampling algorithms to efficiently approximate the maximum likelihood estimate in logistic regression. We first establish consistency and asymptotic normality of the estimator from a general subsampling algorithm, and then derive optimal subsampling probabilities that minimize the asymptotic mean squared error of the resultant estimator. An alternative minimization criterion is also proposed to further reduce the computational cost. The optimal subsampling probabilities depend on the full data estimate, so we develop a two-step algorithm to approximate the optimal subsampling procedure. This algorithm is computationally efficient and has a significant reduction in computing time compared to the full data approach. Consistency and asymptotic normality of the estimator from a two-step algorithm are also established. Synthetic and real data sets are used to evaluate the practical performance of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge