Optimal Randomized First-Order Methods for Least-Squares Problems
Paper and Code
Feb 26, 2020

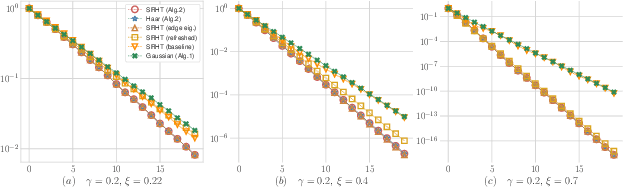
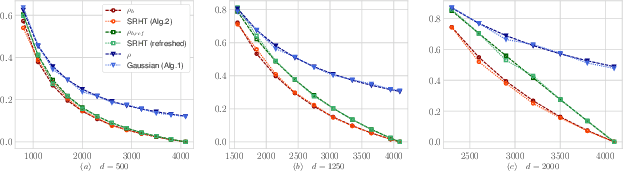
We provide an exact analysis of a class of randomized algorithms for solving overdetermined least-squares problems. We consider first-order methods, where the gradients are pre-conditioned by an approximation of the Hessian, based on a subspace embedding of the data matrix. This class of algorithms encompasses several randomized methods among the fastest solvers for least-squares problems. We focus on two classical embeddings, namely, Gaussian projections and subsampled randomized Hadamard transforms (SRHT). Our key technical innovation is the derivation of the limiting spectral density of SRHT embeddings. Leveraging this novel result, we derive the family of normalized orthogonal polynomials of the SRHT density and we find the optimal pre-conditioned first-order method along with its rate of convergence. Our analysis of Gaussian embeddings proceeds similarly, and leverages classical random matrix theory results. In particular, we show that for a given sketch size, SRHT embeddings exhibits a faster rate of convergence than Gaussian embeddings. Then, we propose a new algorithm by optimizing the computational complexity over the choice of the sketching dimension. To our knowledge, our resulting algorithm yields the best known complexity for solving least-squares problems with no condition number dependence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge