Optimal Order of Encoding for Gaussian MIMO Multi-Receiver Wiretap Channel

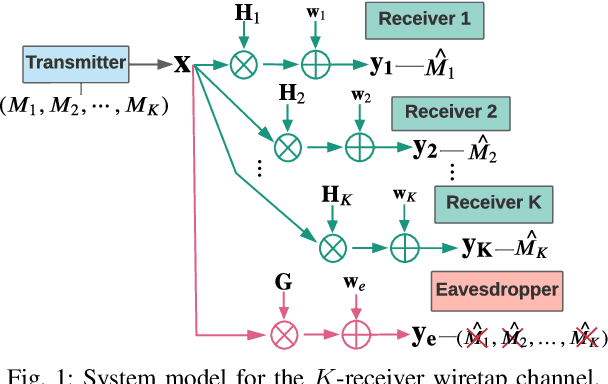
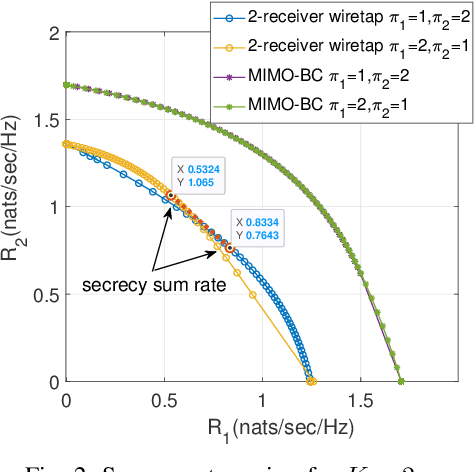
The Gaussian multiple-input multiple-output (MIMO) multi-receiver wiretap channel is studied in this paper. The base station broadcasts confidential messages to K intended users while keeping the messages secret from an eavesdropper. The capacity of this channel has already been characterized by applying dirty-paper coding and stochastic encoding. However, K factorial encoding orders may need to be enumerated for that, which makes the problem intractable. We prove that there exists one optimal encoding order and reduced the K factorial times to a one-time encoding. The optimal encoding order is proved by forming a secrecy weighted sum rate (WSR) maximization problem. The optimal order is the same as that for the MIMO broadcast channel without secrecy constraint, that is, the weight of users' rate in the WSR maximization problem determines the optimal encoding order. Numerical results verify the optimal encoding order.