Optimal Fair Multi-Agent Bandits

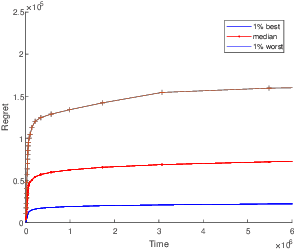
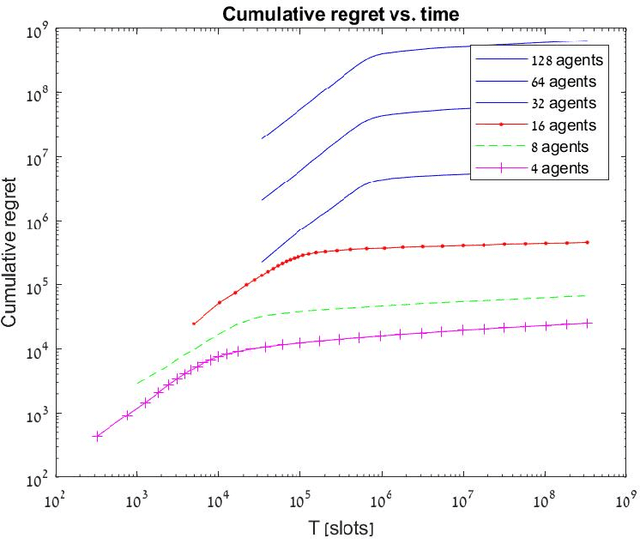
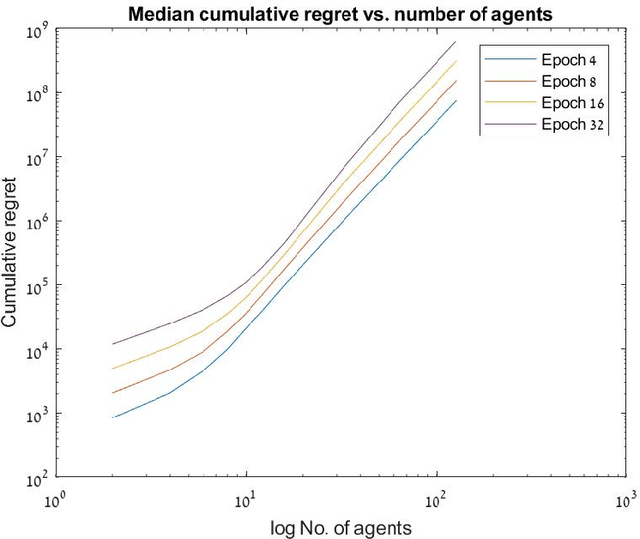
In this paper, we study the problem of fair multi-agent multi-arm bandit learning when agents do not communicate with each other, except collision information, provided to agents accessing the same arm simultaneously. We provide an algorithm with regret $O\left(N^3 \log N \log T \right)$ (assuming bounded rewards, with unknown bound). This significantly improves previous results which had regret of order $O(\log T \log\log T)$ and exponential dependence on the number of agents. The result is attained by using a distributed auction algorithm to learn the sample-optimal matching, a new type of exploitation phase whose length is derived from the observed samples, and a novel order-statistics-based regret analysis. Simulation results present the dependence of the regret on $\log T$.