Optical ISAC: Fundamental Performance Limits and Transceiver Design

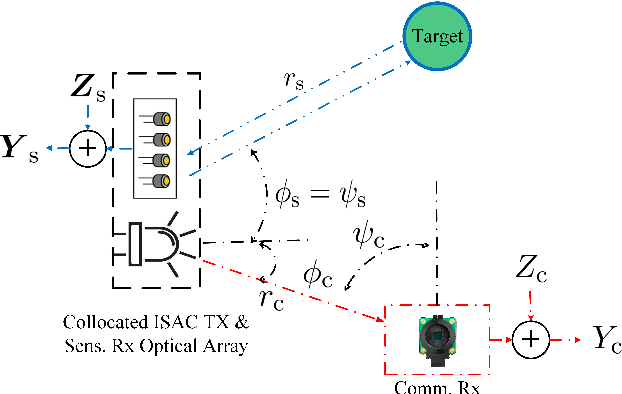
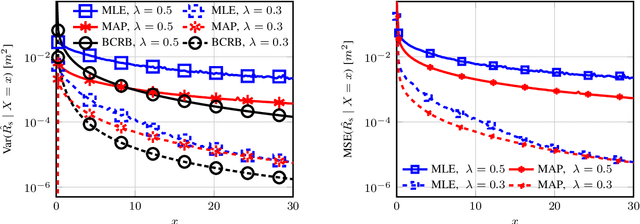
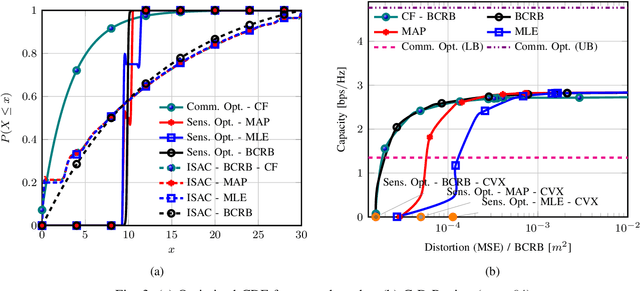
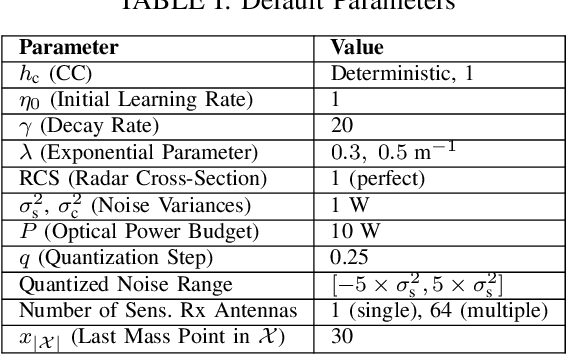
This paper characterizes the optimal capacity-distortion (C-D) tradeoff in an optical point-to-point (P2P) system with single-input single-output for communication and single-input multiple-output for sensing (SISO-COM and SIMO-SEN) within an integrated sensing and communication (ISAC) framework. We consider the optimal rate-distortion (R-D) region and explore several inner (IB) and outer (OB) bounds. We introduce practical, asymptotically optimal maximum a posteriori (MAP) and maximum likelihood estimators (MLE) for target distance, addressing nonlinear measurement-to-state relationships and non-conjugate priors. As the number of sensing antennas increases, these estimators converge to the Bayesian Cram\'er-Rao bound (BCRB). We also establish that the achievable rate-CRB (AR-CRB) serves as an OB for the optimal C-D region, valid for both unbiased estimators and asymptotically large numbers of receive antennas. To clarify that the input distribution determines the tradeoff across the Pareto boundary of the C-D region, we propose two algorithms: \textit{i}) an iterative Blahut-Arimoto algorithm (BAA)-type method, and \textit{ii}) a memory-efficient closed-form (CF) approach. The CF approach includes a CF optimal distribution for high optical signal-to-noise ratio (O-SNR) conditions. Additionally, we adapt and refine the Deterministic-Random Tradeoff (DRT) to this optical ISAC context.