Online Optimization with Untrusted Predictions
Paper and Code
Feb 07, 2022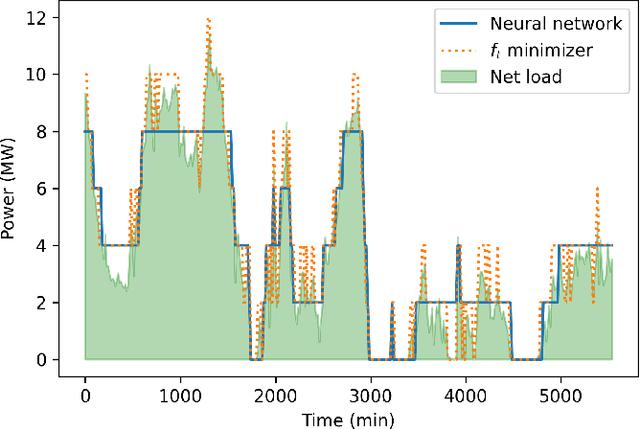
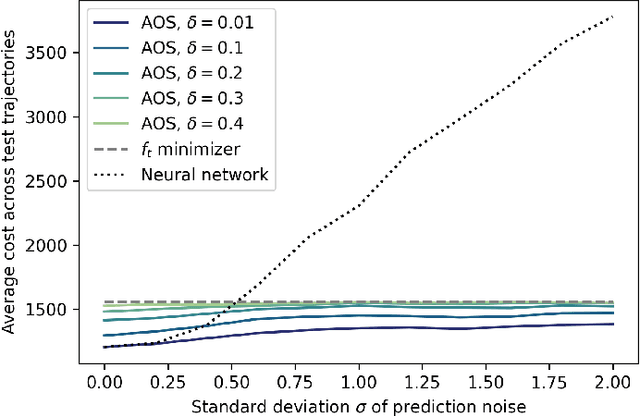
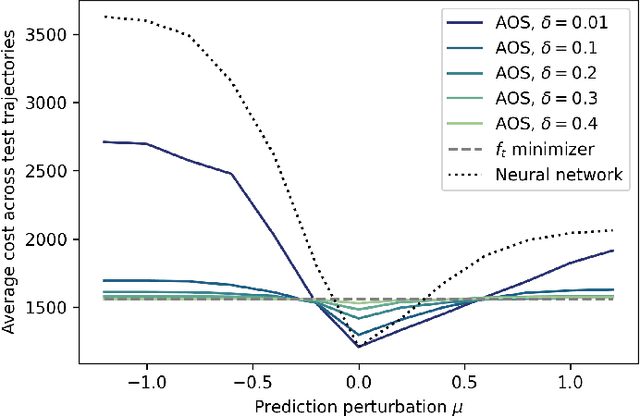
We examine the problem of online optimization, where a decision maker must sequentially choose points in a general metric space to minimize the sum of per-round, non-convex hitting costs and the costs of switching decisions between rounds. The decision maker has access to a black-box oracle, such as a machine learning model, that provides untrusted and potentially inaccurate predictions of the optimal decision in each round. The goal of the decision maker is to exploit the predictions if they are accurate, while guaranteeing performance that is not much worse than the hindsight optimal sequence of decisions, even when predictions are inaccurate. We impose the standard assumption that hitting costs are globally $\alpha$-polyhedral. We propose a novel algorithm, Adaptive Online Switching (AOS), and prove that, for any desired $\delta > 0$, it is $(1+2\delta)$-competitive if predictions are perfect, while also maintaining a uniformly bounded competitive ratio of $2^{\tilde{\mathcal{O}}(1/(\alpha \delta))}$ even when predictions are adversarial. Further, we prove that this trade-off is necessary and nearly optimal in the sense that any deterministic algorithm which is $(1+\delta)$-competitive if predictions are perfect must be at least $2^{\tilde{\Omega}(1/(\alpha \delta))}$-competitive when predictions are inaccurate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge