Online Fault Tolerance Strategy for Abrupt Reachability Constraint Changes
Paper and Code
Jan 03, 2025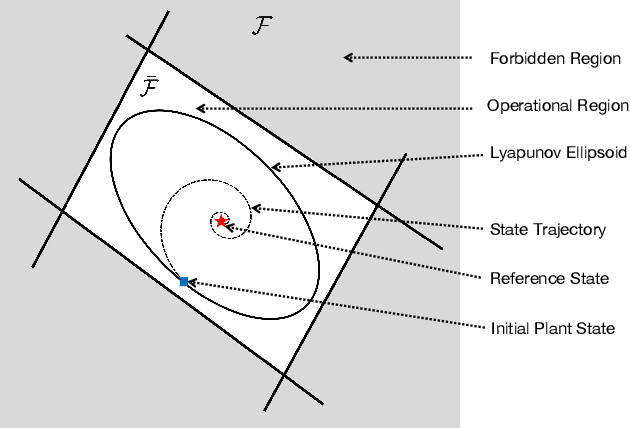
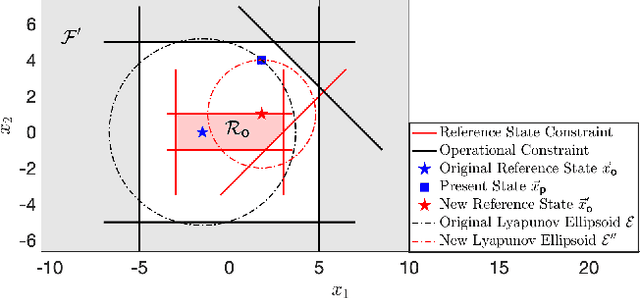
When a system's constraints change abruptly, the system's reachability safety does no longer sustain. Thus, the system can reach a forbidden/dangerous value. Conventional remedy practically involves online controller redesign (OCR) to re-establish the reachability's compliance with the new constraints, which, however, is usually too slow. There is a need for an online strategy capable of managing runtime changes in reachability constraints. However, to the best of the authors' knowledge, this topic has not been addressed in the existing literature. In this paper, we propose a fast fault tolerance strategy to recover the system's reachability safety in runtime. Instead of redesigning the system's controller, we propose to change the system's reference state to modify the system's reachability to comply with the new constraints. We frame the reference state search as an optimization problem and employ the Karush-Kuhn-Tucker (KKT) method as well as the Interior Point Method (IPM) based Newton's method (as a fallback for the KKT method) for fast solution derivation. The optimization also allows more future fault tolerance. Numerical simulations demonstrate that our method outperforms the conventional OCR method in terms of computational efficiency and success rate. Specifically, the results show that the proposed method finds a solution $10^{2}$ (with the IPM based Newton's method) $\sim 10^{4}$ (with the KKT method) times faster than the OCR method. Additionally, the improvement rate of the success rate of our method over the OCR method is $40.81\%$ without considering the deadline of run time. The success rate remains at $49.44\%$ for the proposed method, while it becomes $0\%$ for the OCR method when a deadline of $1.5 \; seconds$ is imposed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge