Online Expectation-Maximization Based Frequency and Phase Consensus in Distributed Phased Arrays
Paper and Code
Jul 26, 2022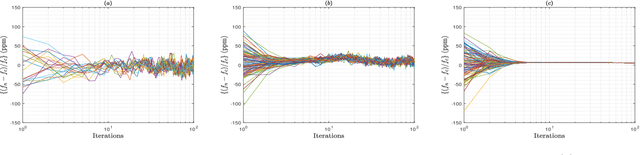

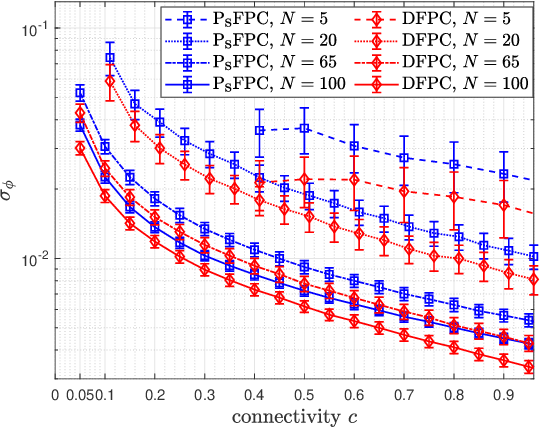
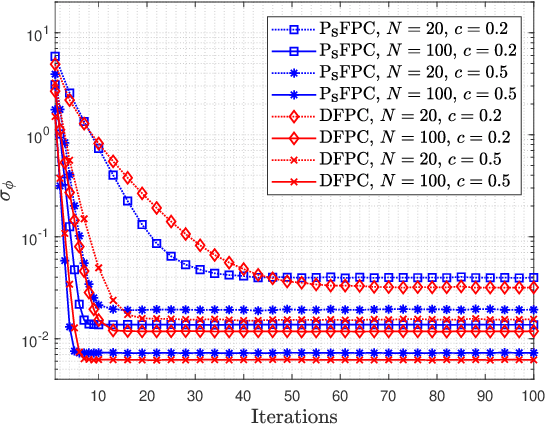
Distributed phased arrays are comprised of separate, smaller antenna systems that coordinate with each other to support coherent beamforming towards a destination. However, due to the frequency drift and phase jitter of the oscillators, as well as the frequency and phase estimation errors induced at the nodes, there exists decoherence that degrades the beamforming process. A decentralized frequency and phase consensus (DFPC) algorithm was proposed in prior work for undirected networks in which the nodes locally share their frequencies and phases with their neighbors to reach synchronization. Kalman filtering (KF) was also integrated with DFPC (KF-DFPC) to lower the total residual phase error upon convergence. Since these DFPC-based algorithms rely on the average consensus protocol, they do not converge for directed networks. In this paper, we propose a push-sum based frequency and phase consensus (PsFPC) algorithm for the directed networks. The residual phase error of PsFPC is theoretically derived as well. Kalman filtering is also integrated with PsFPC and the resulting KF-PsFPC algorithm shows a significant reduction in the residual phase error upon convergence. KF assumes that the model parameters, i.e., the measurement noise and innovation noise covariance matrices, are known. Since they may not be known in practice, we develop an online expectation maximization (EM) based algorithm that iteratively computes the maximum likelihood (ML) estimate of the unknown matrices in an online manner. EM is integrated with KF-PsFPC to propose the EM-KF-PsFPC algorithm. Simulation results are included where the performance of the PsFPC-based algorithms is analyzed for different distributed phased arrays and is compared to other algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge