Online control of the familywise error rate

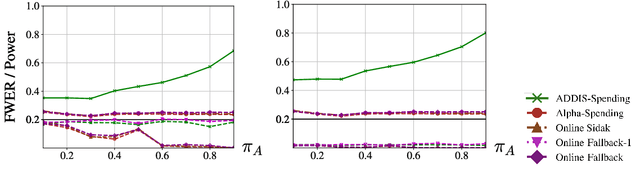
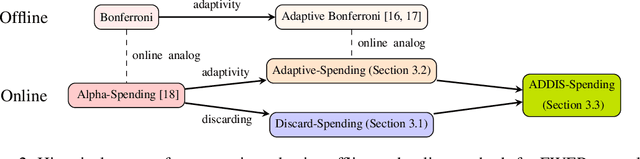
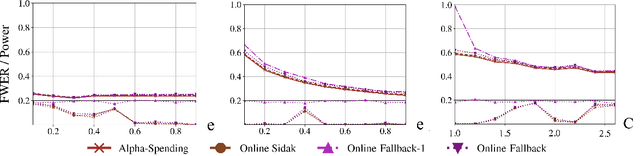
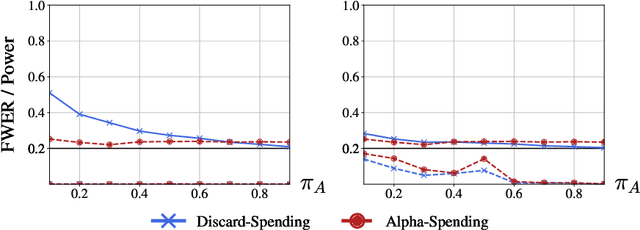
Suppose an analyst wishes to test an infinite sequence of hypotheses one by one over time in such a way that the familywise error rate (FWER) is controlled at level $\alpha$. Specifically, without knowing the future $p$-values, the analyst must irrevocably decide at each step whether to reject the null, such that with probability at least $1-\alpha$, there are no false rejections in the entire sequence. This paper unifies algorithm design concepts developed for offline FWER control and for online false discovery rate (FDR) control. Though Bonferroni, fallback procedures and Sidak's method can trivially be extended to the online setting, our main contribution is the design of new, adaptive online algorithms that control the FWER and per-family error rate (PFER) when the $p$-values are independent or locally dependent in time. Our experiments demonstrate substantial gains in power, also formally proved in an idealized Gaussian model.