On Two Distinct Sources of Nonidentifiability in Latent Position Random Graph Models
Paper and Code
Mar 31, 2020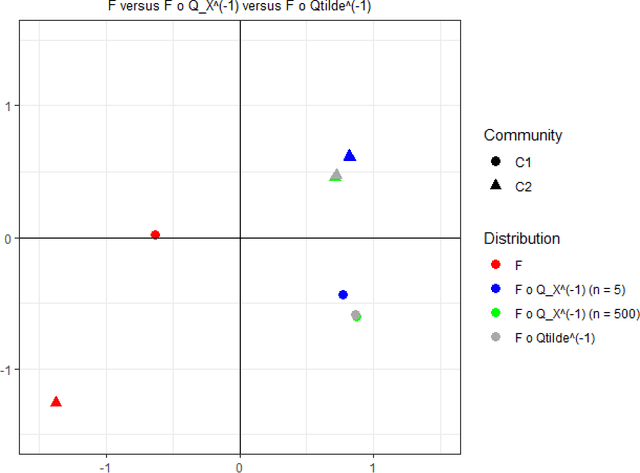
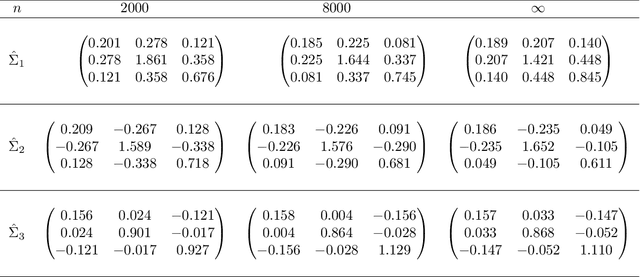
Two separate and distinct sources of nonidentifiability arise naturally in the context of latent position random graph models, though neither are unique to this setting. In this paper we define and examine these two nonidentifiabilities, dubbed subspace nonidentifiability and model-based nonidentifiability, in the context of random graph inference. We give examples where each type of nonidentifiability comes into play, and we show how in certain settings one need worry about one or the other type of nonidentifiability. Then, we characterize the limit for model-based nonidentifiability both with and without subspace nonidentifiability. We further obtain additional limiting results for covariances and $U$-statistics of stochastic block models and generalized random dot product graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge