On the Structure of the Time-Optimal Path Parameterization Problem with Third-Order Constraints
Paper and Code
Sep 19, 2017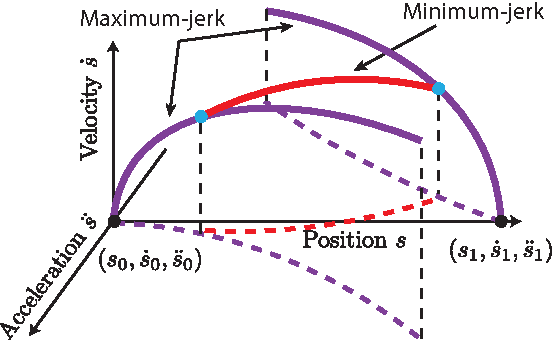
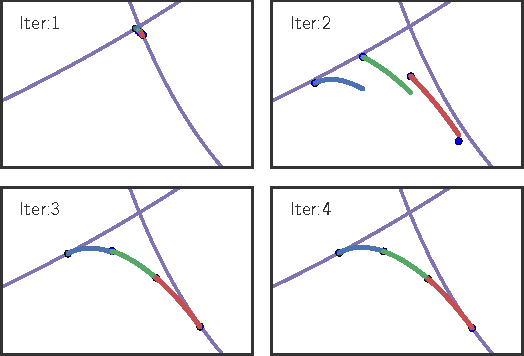
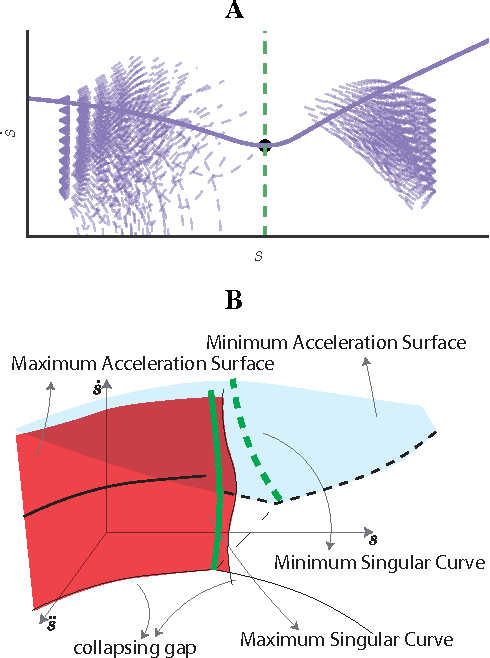

Finding the Time-Optimal Parameterization of a Path (TOPP) subject to second-order constraints (e.g. acceleration, torque, contact stability, etc.) is an important and well-studied problem in robotics. In comparison, TOPP subject to third-order constraints (e.g. jerk, torque rate, etc.) has received far less attention and remains largely open. In this paper, we investigate the structure of the TOPP problem with third-order constraints. In particular, we identify two major difficulties: (i) how to smoothly connect optimal profiles, and (ii) how to address singularities, which stop profile integration prematurely. We propose a new algorithm, TOPP3, which addresses these two difficulties and thereby constitutes an important milestone towards an efficient computational solution to TOPP with third-order constraints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge