On the Statistical and Information-theoretic Characteristics of Deep Network Representations

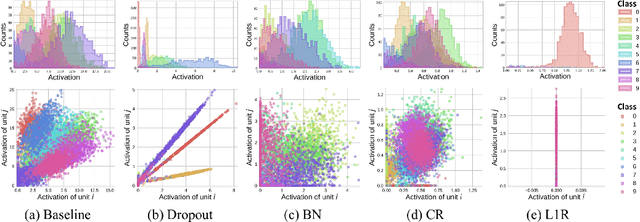
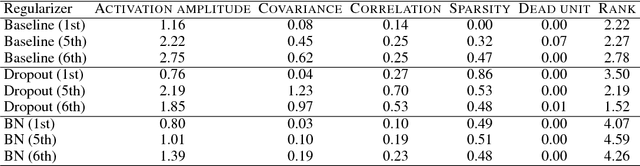
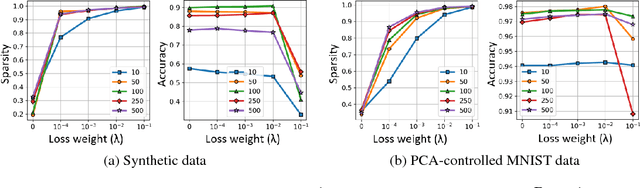
It has been common to argue or imply that a regularizer can be used to alter a statistical property of a hidden layer's representation and thus improve generalization or performance of deep networks. For instance, dropout has been known to improve performance by reducing co-adaptation, and representational sparsity has been argued as a good characteristic because many data-generation processes have a small number of factors that are independent. In this work, we analytically and empirically investigate the popular characteristics of learned representations, including correlation, sparsity, dead unit, rank, and mutual information, and disprove many of the \textit{conventional wisdom}. We first show that infinitely many Identical Output Networks (IONs) can be constructed for any deep network with a linear layer, where any invertible affine transformation can be applied to alter the layer's representation characteristics. The existence of ION proves that the correlation characteristics of representation is irrelevant to the performance. Extensions to ReLU layers are provided, too. Then, we consider sparsity, dead unit, and rank to show that only loose relationships exist among the three characteristics. It is shown that a higher sparsity or additional dead units do not imply a better or worse performance when the rank of representation is fixed. We also develop a rank regularizer and show that neither representation sparsity nor lower rank is helpful for improving performance even when the data-generation process has a small number of independent factors. Mutual information $I(\mathbf{z}_l;\mathbf{x})$ and $I(\mathbf{z}_l;\mathbf{y})$ are investigated, and we show that regularizers can affect $I(\mathbf{z}_l;\mathbf{x})$ and thus indirectly influence the performance. Finally, we explain how a rich set of regularizers can be used as a powerful tool for performance tuning.