On the Robustness of Deep Learning-predicted Contention Models for Network Calculus

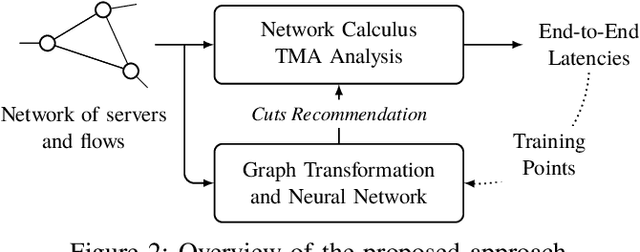
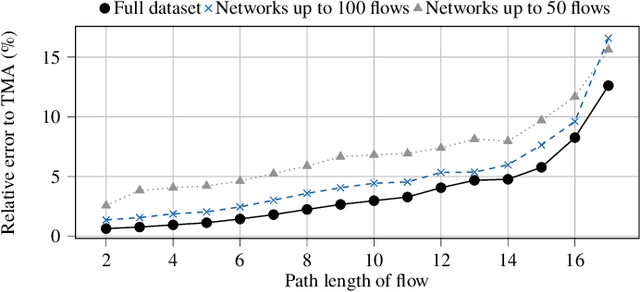
The network calculus (NC) analysis takes a simple model consisting of a network of schedulers and data flows crossing them. A number of analysis "building blocks" can then be applied to capture the model without imposing pessimistic assumptions like self-contention on tandems of servers. Yet, adding pessimism cannot always be avoided. To compute the best bound on a single flow's end-to-end delay thus boils down to finding the least pessimistic contention models for all tandems of schedulers in the network - and an exhaustive search can easily become a very resource intensive task. The literature proposes a promising solution to this dilemma: a heuristic making use of machine learning (ML) predictions inside the NC analysis. While results of this work are promising in terms of delay bound quality and computational effort, there is little to no insight on why a prediction is made or if the trained machine can achieve similarly striking results in networks vastly differing from its training data. In this paper we address these pending questions. We evaluate the influence of the training data and its features on accuracy, impact and scalability. Additionally, we contribute an extension of the method by predicting the best $n$ contention model alternatives in order to achieve increased robustness for its application outside the training data. Our numerical evaluation shows that good accuracy can still be achieved on large networks although we restrict the training to networks that are two orders of magnitude smaller.